Kezdőlap


Feladat:	Pontversenyen kívüli P.30	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Göndőcs Ferenc , Simon Júlia , Somorjai Gábor , Vajnági András , Váli László
Füzet:	1970/január, 24 - 25. oldal		PDF \| MathML
Témakör(ök):	Alakzatba írt kör, Szélsőérték differenciálszámítással, Trigonometriai azonosságok, Hossz, kerület, Terület, felszín, Szögfüggvények, síkgeometriai számítások, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1969/április: Pontversenyen kívüli P.30

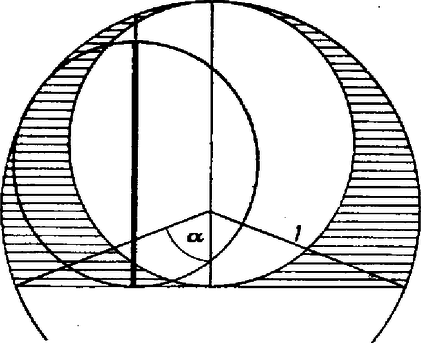
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A kör sugarát 1-nek választjuk, és a kérdéses húrt a hozzá tartozó $2 α (< π)$ középponti szöggel határozzuk meg. A szeletbe beírt ‐ vagyis mind a húrt, mind az ívet érintő ‐ kör átmérője nem lehet nagyobb, mint a húrra az érintkezési pontban állított merőlegesnek a szeletbe eső szakasza. Ez a szakasz akkor a legnagyobb, ha rajta van a szelet szimmetriatengelyén, és ebben a helyzetben a szakasz, mint átmérő fölé írt kör egyszersmind maga a beírt kör; ezt kell tehát tekintenünk.

A körszelet területe

π - (α - sin α cos α)

, a beírt kör területe

π {(1 + cos α)}^{2} / 4

, ezekből a kérdéses terület kifejezése így alakítható:

\begin{matrix} t = \frac{3 π}{4} - α - \frac{π}{2} cos α - \frac{π}{4} cos^{2} α + sin α cos α . \end{matrix}

A kívánt maximumot a derivált eltűnése alapján keressük.

\begin{matrix} t' = & - 1 + \frac{π}{2} sin α + \frac{π}{2} sin α cos α + cos^{2} α - sin^{2} α = \\ = \frac{π}{2} sin α (1 + cos α - \frac{4}{π} sin α) = \\ = \frac{π}{2} sin α (2 cos^{2} \frac{α}{2} - \frac{8}{π} sin \frac{α}{2} cos \frac{α}{2}) = \\ = π sin α cos \frac{α}{2} (cos \frac{α}{2} - \frac{4}{π} sin \frac{α}{2}) . \end{matrix}

Ennek az első két (változó) tényező eltűnéséből adódó zérushelyei számunkra. érdektelenek:

sin α = 0

esetén

α = 0

, a húr hossza

0

, a szelet azonos az adott körrel, a beírt kör ezt egészen kitölti, a vizsgált terület

0

;

cos α / 2 = 0

gyöke pedig nem a figyelembe vett tartományba esik. A zárójeles tényező akkor és csak akkor tűnik el, ha

\begin{matrix} tg \frac{α}{2} = \frac{π}{4} \approx 0, 5708. \end{matrix}

(1)

Ezen a helyen a derivált csökkenve halad át, mert a zárójelben

cos α / 2

csökken, ugyanígy a második tag is, hiszen

sin α / 2

növekvő, az elöl álló tényezők pedig pozitívok. Eszerint az (1)-gyel meghatározott szög esetében a vizsgált területnek maximuma van.
A maximum helyén a húr hossza

\begin{matrix} 2 sin α = \frac{4 tg α / 2}{1 + {tg}^{2} α / 2} = \frac{16 π}{16 + π^{2}} \approx 1, 943 \end{matrix}

(α = 76^{\circ} 17, 5') .

Vajnági András (Budapest, Fazekas M. Gyak. Gimn.)