Kezdőlap


Feladat:	Pontversenyen kívüli P.17	Korcsoport: -	Nehézségi fok: nehéz
Megoldó(k):	Beck József , Horváth László , Reviczky János
Füzet:	1969/május, 218 - 219. oldal		PDF \| MathML
Témakör(ök):	Síkbeli ponthalmazok távolsága, Négyzetrács geometriája, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1969/január: Pontversenyen kívüli P.17

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

a feladat a) részére. Tájékozódásul beírjuk az útvonal első 59 rácspontjához tartozó lépésszámokat a koordinátarendszerbe¹ (1. ábra).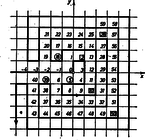

1. ábra

A (

k, k

) rácspontokhoz rendelt számok

k

első 5 értékére:

\begin{matrix} 2, 14, 26, 58, 82, ... \end{matrix}

(1)

Ezekbe a pontokba a bolyongás során nem azonos irányból érkezünk meg: a 2., 26., 82.,

...

pontba balról futunk be, a 14., 58.,

...

pontba pedig alulról. Ennek megfelelően a (

k k

) pontból a (

k + 1, k + 1

) pontig futó útvonalrész is kétféle aszerint, hogy

k

páratlan-e vagy páros (2. ábra). Az első esetben lefelé indulunk, a másodikban balra.

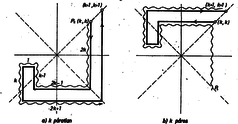2. ábra

A kétféle útvonalrész jobban hasonlítana egymáshoz, ha az első útvonalrész utolsó szakaszát elhagynánk, a másodikat pedig kiegészítenénk egy megfelelő kezdő útszakasszal; a módosított útvonalrészt az ábra hullámos vonallal mutatja. Így a (

k, k

) pontot a (

k, - k

) ponttal helyettesítjük, ha

k

páros, jelöljük ezt a pontot

P_{k}

-val; ha pedig

k

páratlan,

P_{k}

jelölje az eredeti (

k, k

) pontot. Így a

P_{k}

pontok

N (k)

sorszámai

k

első 5 értékére:

\begin{matrix} 2, 10, 26, 50, 82, ... \end{matrix}

(2)

P_{k}

pontból indulva (

k > 1

esetén) először annak a

Q_{k}

négyzetnek a kerületén haladunk, melynek

P_{k}

az egyik csúcsa és középpontja az origó. Függőlegesen

2 k

lépést, majd vízszintesen 1-gyel kevesebbet,

2 k - 1

lépést teszünk meg, és áttérünk a

P_{k - 1}

-re támaszkodó

Q_{k - 1}

négyzetre,

k - 1

lépés után az

x

tengely mellé érünk, visszatérünk

Q_{k}

peremére 1 lépéssel, azon függőlegesen haladva

k

lépéssel elérjük

Q_{k + 1}

peremét és ennek vízszintes szakaszán fejezzük be utunkat,

2 k + 1

lépéssel elérjük

P_{k + 1}

-et. A

P_{k}

-ból

P_{k + 1}

-be vezető útvonalrész tehát

\begin{matrix} 2 k + (2 k - 1) + (k - 1) + 1 + k + (2 k + 1) = 8 k \end{matrix}

lépésből áll, azaz

\begin{matrix} N (k + 1) - N (k) = 8 k . \end{matrix}

(3)

Közvetlenül leszámolhatjuk, hogy az eredmény

k = 1

esetén is érvényes.
Mármost a (3) egyenletet

k = 1, 2, ..., l - 1

esetére felírva és összeadva kapjuk, hogy

\begin{matrix} N (l) - N (1) = 8 \cdot 1 + 8 \cdot 2 + ... + 8 (l - 1) = 4 l^{2} - 4 l, \\ N (l) = 4 l^{2} - 4 l + 2, & (4) \end{matrix}

hiszen

N (1) = 2

.
Ha

l

páratlan, akkor

P_{l}

az (

l, l

) ponttal azonos; tehát (4) megadja a keresett sorszámot. Ha

l

páros, az (

l, l

) pontot csak

P_{l}

, után

2 l

lépéssel érjük el, így végül az (

l, l

) pont

M (l)

sorszáma:

\begin{matrix} M (l) = {\begin{matrix} N (l) = 4 l^{2} - 4 l + 2, & ha l páratlan, & (5) \\ N (l) + 2 l = 4 l^{2} - 2 l + 2, & ha l páros. \end{matrix} \end{matrix}

Megoldotta a feladat a) részét: Beek József, Horváth László, Reviczky János.
A feladat b) részére nem érkezett megoldás, így annak megoldását e szám feladataival együtt elfogadjuk.

¹A kitűzés eredeti ábráján a számok csak 7-ig voltak beírva. (Szerk.)