Kezdőlap


Feladat:	Pontversenyen kívüli P.13	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Beck József , Csirmaz László , Göndőcs Ferenc , Somorjai Gábor
Füzet:	1969/szeptember, 22 - 25. oldal		PDF \| MathML
Témakör(ök):	Konstruktív megoldási módszer, Két pont távolsága, szakasz hosszúsága, Ponthalmazok távolsága, Szimmetrikus alakzatok, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1968/december: Pontversenyen kívüli P.13

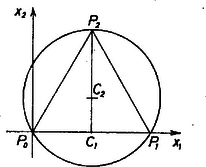
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Jelöljük $C_{2}$ -vel $P_{3}$ merőleges vetületét a $P_{0}$ , $P_{1}$ , $P_{2}$ pontok síkján; határozzuk meg először ennek a koordinátáit. Megmutatjuk, hogy $C_{2}$ a $P_{0} P_{1} P_{2}$ háromszög köré írható kör középpontja. A $P_{i} C_{2} P_{3}$ háromszögek $(i = 0,1,2)$ ugyanis derékszögűek, tehát

\begin{matrix} P_{i} C_{2}^{2} + C_{2} P_{3}^{2} = P_{i} P_{3}^{2}, (i = 0,1,2) \end{matrix}

(2)

ahol a jobb oldalon az előírás szerint

1

áll. Jelöljük a

C_{2} P_{3}

szakasznak, a keresett tetraéder magasságának hosszát

m_{3}

-mal. Ekkor (2) alapján

\begin{matrix} P_{i} C_{2}^{2} = 1 - m_{3}^{2}, (i = 0,1,2) \end{matrix}

ami állításunkat igazolja.

C_{2}

P_{2}

pontok egyenlő távolságra vannak a

P_{0}

P_{1}

pontoktól, a

P_{0} P_{1}

szakaszra eső vetületük tehát e szakasz

C_{1}

felezőpontjával azonos. Jelöljük a

C_{2}

pont koordinátáit

(c_{1}, c_{2},0)

-val. Mivel

P_{0} P_{1} P_{2}

szabályos háromszög,

\begin{matrix} c_{1} = \frac{1}{2}, c_{2} = \frac{1}{3} C_{1} P_{2} = \frac{1}{3} m_{2} = \frac{1}{2 \sqrt[]{3}}, \end{matrix}

és (3) alapján

\begin{matrix} m_{3}^{2} = 1 - P_{0} C_{2}^{2} = 1 - c_{1}^{2} - c_{2}^{2} = \frac{2}{3} . \end{matrix}

Ezek szerint a

P_{3}

pont koordinátái

(\frac{1}{2}, \frac{1}{2 \sqrt[]{3}}, \sqrt[]{\frac{2}{3}})

.
II. Jelöljük a keresett

R_{j}

pontok (

j = 0,1,2, ..., n

) koordinátáit (

x_{j 1}, x_{j 2}, ..., x_{j n}

)-nel. A feladat szerint

\begin{matrix} x_{j i} > 0 ha 1 \leq i \leq j és x_{j i} = 0, ha j < i \leq n \end{matrix}

Tegyük fel, hogy már meghatároztuk ezeket a pontokat úgy, hogy bármelyik két pont távolsága

1

. Megmutatjuk, hogy tetszőleges

0 \leq j \leq n

mellett pontosan egy olyan

C_{j}

pont van, melynek csak az első

j

koordinátája különbözik

0

-tól és az

R_{0}, R_{1}, ..., R_{j}

pontoktól egyenlő távolságra van.
A

C_{0}

pontnak minden koordinátája

0

, tehát azonos

P_{0}

-lal,

C_{1}

-nek csak az első koordinátája nem

0

, és

P_{0}

-tól,

P_{1}

-től egyenlő távolságra van, így ez az első koordináta csak

1 / 2

lehet.
Tegyük fel, hogy állításunk helyes minden

j \leq k

értékre, és a

Q

(y_{1}, y_{2}, ..., y_{n})

pont egyenlő távolságra van az

R_{0}, R_{1}, ..., R_{k}

pontoktól. Ha

i \leq k

, akkor az

R_{i}

Q

pontok távolsága (1) szerint

\begin{matrix} R_{i} Q^{2} = {(x_{i 1} - y_{1})}^{2} + ... + {(x_{i k} - y_{k})}^{2} + y_{k + 1}^{2} + ... + y_{n}^{2}, \end{matrix}

(4)

hiszen

x_{i l} = 0

, ha

l > k \geq i

. A

Q'

(y_{1}, y_{2}, ..., y_{k},0, ...,0)

pontnak pedig az

R_{i}

ponttól mért távolsága

\begin{matrix} R_{i} Q'^{2} = {(x_{i} - y_{1})}^{2} + ... + {(x_{i k} - y_{k})}^{2} . \end{matrix}

(5)

(4)-ből (5)-öt kivonva kapjuk, hogy

\begin{matrix} R_{i} Q^{2} - R_{i} Q'^{2} = y_{k + 1}^{2} + ... + y_{n}^{2}, \\ R_{i} Q'^{2} = R_{i} Q^{2} - (y_{k + 1}^{2} + ... + y_{n}^{2}) . & (6) \end{matrix}

Q'

pont tehát egyenlő távolságra van az

R_{0}, R_{1}, ..., R_{k}

pontoktól, így azonos

C_{k}

-val, azaz minden olyan

Q

pont első

k

koordinátája egyenlő a

C_{k}

pont első

k

koordinátájával, amely az

R_{0}, R_{1}, ..., R_{k}

pontoktól egyenlő távolságra van.
Jelöljük a

C_{k}

pont koordinátáit

(c_{1}, c_{2}, ..., c_{k},0,0, ...,0)

-val, és legyen a

C_{k + 1}

pont egyenlő távolságra az

R_{0}, R_{1}, ... R_{k + 1}

pontoktól. A fentiek alapján

C_{k + 1}

első

k

koordinátája megegyezik

C_{k}

koordinátáival, jelöljük a

(k + 1)

-iket

c_{k + 1}

-gyel, és tegyük fel, hogy a többi koordináta

0

. Megmutatjuk, hogy

C_{k + 1}

egyértelműen meg van határozva.
Mivel az

R_{k + 1}

pont is egyenlő távolságra van az

R_{0}, R_{1}, ..., R_{k}

pontoktól,

R_{k + 1}

első

k

koordinátája is megegyezik

C_{k}

koordinátáival; jelöljük

R_{k + 1}

(k + 1)

-ik koordinátáját

m_{k + 1}

-gyel. (6) alapján a

Q = C_{k + 1}

pontra kapjuk, hogy ha

i \leq k

\begin{matrix} R_{i} C_{k + 1}^{2} - R_{i} C_{k}^{2} = c_{k + 1}^{2}, \end{matrix}

(7)

Q = R_{k + 1}

pontra pedig

\begin{matrix} R_{i} R_{k + 1}^{2} - R_{i} C_{k}^{2} = m_{k + 1}^{2} . \end{matrix}

(8)

(8) és (7) különbségébe az

\begin{matrix} R_{i} C_{k + 1}^{2} = R_{k + 1} C_{k + 1}^{2} = {(m_{k + 1} - c_{k + 1})}^{2} \end{matrix}

értéket helyettesítve kapjuk, hogy

\begin{matrix} {(m_{k + 1} - c_{k + 1})}^{2} - 1 = c_{k + 1}^{2} - m_{k + 1}^{2}, \\ c_{k + 1} = \frac{2 m_{k + 1}^{2} - 1}{2 m_{k + 1}}, & (9) \end{matrix}

C_{k + 1}

pontot tehát valóban egyértelműen meghatározzák az

R_{0}, R_{1}, ..., R_{k}

pontok.
Azt is kaptuk, hogy ha

i < j

, akkor

C_{j}

első

i

koordinátája megegyezik

C_{i}

első

i

koordinátájával, és

R_{j}

első

j - 1

koordinátája megegyezik

C_{j - 1}

első

j - 1

koordinátájával. Az

R_{j}

pont koordinátái tehát:

\begin{matrix} x_{j 1} = c_{1}, x_{j 2} = c_{2}, ..., x_{j, j - 1} = c_{j - 1}, x_{j j} = m_{j}, x_{j, j + 1} = ... = x_{j n} = 0, \end{matrix}

(10)

ahol a

c_{i}

és

m_{i}

együtthatók kapcsolatát (9) adja meg. (10) és (1) alapján

R_{j}

és

R_{j + 1}

távolságára kapjuk, hogy

\begin{matrix} m_{j + 1}^{2} + {(m_{j} - c_{j})}^{2} = 1, \end{matrix}

(11)

amiből, (9)-et felhasználva rekurziót kaphatunk az

m_{j}

számokra:

\begin{matrix} m_{j + 1}^{2} = 1 - {(m_{j} - c_{j})}^{2} = m_{j}^{2} - c_{j}^{2} = m_{j}^{2} - {(m_{j} - \frac{1}{2 m_{j}})}^{2} = 1 - \frac{1}{{(2 m_{j})}^{2}} . \end{matrix}

(12)

m_{1} = 1

értékből kiindulva kapjuk, hogy

\begin{matrix} m_{2}^{2} = 1 - \frac{1}{4} = \frac{3}{4}, m_{3}^{2} = 1 - \frac{1}{3} = \frac{2}{3} = \frac{4}{6}, m_{4}^{2} = 1 - \frac{3}{8} = \frac{5}{8}, \end{matrix}

ezek alapján azt sejtjük, hogy

\begin{matrix} m_{k}^{2} = \frac{k + 1}{2 k} . \end{matrix}

(13)

Ezt (12) alapján teljes indukcióval bizonyítjuk be.

\begin{matrix} m_{k + 1}^{2} = 1 - \frac{1}{4} \cdot \frac{1}{m_{k}^{2}} = 1 - \frac{1}{4} \cdot \frac{2 k}{k + 1} = \frac{2 k + 2 - k}{2 (k + 1)} = \frac{k + 2}{2 (k + 1)} . \end{matrix}

Végül (13) és (9) alapján

\begin{matrix} c_{k} = \frac{1}{k} \sqrt[]{\frac{k}{2 (k + 1)}} = \frac{1}{\sqrt[]{2 k (k + 1)}} . \end{matrix}

(14)

Ha tehát van a feladatnak megoldása, akkor csak a (10), (13), (14) összefüggésekkel megadott koordinátájú pontok felelhetnek meg. Vegyük észre, hogy

\begin{matrix} m_{k} = (k + 1) c_{k} \end{matrix}

(15)

tehát ha

1 \leq i < j \leq n

, az így kapott

R_{i}

R_{j}

pontok távolsága

\begin{matrix} R_{i} R_{j}^{2} = i^{2} c_{i}^{2} + c_{i + 1}^{2} + ... + c_{j - 1}^{2} + {(j + 1)}^{2} c_{j}^{2} = \\ = \frac{i}{2 (i + 1)} + \frac{1}{2 (i + 1) (i + 2)} + ... + \frac{1}{2 (j - 1) j} + \frac{j + 1}{2 j} = \\ = \frac{1}{2} [(1 - \frac{1}{i + 1}) + (\frac{1}{i + 1} - \frac{1}{i + 2}) + ... + (\frac{1}{j - 1} - \frac{1}{j}) + (1 + \frac{1}{j})], \end{matrix}

a kapott pontok tehát valóban megfelelőek.

Megjegyzés. (15) alapján könnyen bizonyítható, hogy a

C_{k}

pont az

R_{0}, R_{1}, ..., R_{k}

pontok ,,súlypontja'', azaz

\begin{matrix} c_{i} = \frac{1}{k + 1} (x_{0 i} + x_{1 i} + ... + x_{k i}) \end{matrix}

i \leq k

Göndőcs Ferenc