Kezdőlap


Feladat:	Pontversenyen kívüli P.7	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Beck József , Göndőcs Ferenc , Somorjai Gábor , Soós Miklós , Váli László
Füzet:	1969/március, 120 - 122. oldal		PDF \| MathML
Témakör(ök):	Pont körüli forgatás, Szimmetrikus sokszögek, Szabályos sokszögek geometriája, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1968/október: Pontversenyen kívüli P.7

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Egy hatszög akkor (és csak akkor) centrálszimmetrikus, ha szemközti oldalai páronként párhuzamosak és egyenlők, ezért elegendő azt bizonyítani, hogy a kiindulási hatszögben ez a tulajdonság fennáll. A bizonyítást vektorokkal végzett számítás útján végezzük el. Ennek során azt a vektort, amely egy tetszés szerinti $v$ vektorból pozitív irányú, $60^{\circ}$ -os elforgatással adódik, $v'$ -vel fogjuk jelölni. Így a $v$ -ből $120^{\circ}$ , $180^{\circ}$ , $240^{\circ}$ , $300^{\circ}$ szögű elforgatással adódó vektor rendre $(v')' = v'' = v' - v$ ; $- v$ , $- v'$ , $v - v'$ (1. ábra).

1. ábra

Legyenek a kiindulási, pozitív körüljárású

A B C D E F

hatszög oldalvektorai rendre

\vec{A B} = a

\vec{B C} = b

...

\vec{F A} = f

, az ezek fölé kifelé szerkesztett szabályos háromszögek új csúcsai rendre

A_{1}

B_{1}

...

F_{1}

, az

A_{1} B_{1}

...

F_{1} A_{1}

oldalfelező pontjai rendre

A_{2}

...

F_{2}

(2. 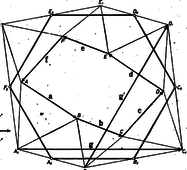ábra).

2. ábra

\vec{A_{2} B_{2}}

\vec{B_{2} C_{2}}

vektor fele akkora, mint

\vec{A_{1} C_{1}}

, ill.

\vec{B_{1} D_{1}}

, a föltevés szerint pedig

\vec{B_{2} C_{2}}

\vec{A_{2} B_{2}}

-ból

+ 60^{\circ}

-os elfordítással áll elő, ezért

\vec{A_{1} C_{1}} = g

jelöléssel

\vec{B_{1} D_{1}} = g'

. Másrészt

\begin{matrix} \vec{A_{1} C_{1}} = \vec{A_{1} B} + \vec{B C} + \vec{C C_{1}}, \end{matrix}

itt

\vec{A_{1} B} = - \vec{B A_{1}} = a'

, és

\vec{C C_{1}} = c - c'

, tehát

\begin{matrix} a' + b + (c - c') = g, \end{matrix}

(1)

és hasonlóan

B_{1} D_{1}

felbontása alapján

\begin{matrix} b' + c + (d - d') = g' . \end{matrix}

(2)

Az utóbbi vektort negatív irányban

60^{\circ}

-kal elfordítva a jobb oldalon visszakapjuk

g

-t, a bal oldal tagjait pedig az 1. ábra szerint képezzük:

\begin{matrix} b + (c - c') - d' = g, \end{matrix}

(3)

és ezt (1)-gyel egybevetve

\begin{matrix} a' = - d', azaz a = - d, \end{matrix}

vagyis szavakkal:

\vec{A B}

és

\vec{D E}

egyenlő irányúak és abszolút értékűek, továbbá ellentétes irányításúak. Ez állításunk része.
Mivel végül

A B

-vel, ill.

a

-val az eredeti hatszög tetszés szerinti oldalát jelöltük, és a feltevés kihasznált része az

A_{2} B_{2} ... F_{2}

hatszög bármelyik két, egymás utáni oldalára fennáll, megállapításunk az eredeti hatszög bármelyik két, szemben fekvő oldalára érvényes, a bizonyítást befejeztük.

Göndőcs Ferenc (Győr, Révai M. Gimn.)

II. megoldás. Az eredeti hatszög csúcsait jelöljük

A_{1}

A_{2}

A_{3}

A_{4}

A_{5}

A_{6}

-tal, az

A_{6} A_{1}

szakasz fölé előírt módon rajzolt szabályos háromszög csúcsát

B_{1}

-gyel,

B_{2}

B_{3}

B_{4}

B_{5}

B_{6}

pedig legyen a további háromszögek csúcsa. A

B_{1} B_{2}

, ill.

A_{1} A_{2}

szakasz felezőpontja legyen

C_{1}

, ill.

D_{1}

, a

C_{2}

C_{3}

C_{4}

;

C_{5}

C_{6}

, ill.

D_{2}

D_{3}

D_{4}

D_{5}

D_{6}

pont pedig a további oldalszakaszok felezőpontja a származtatott, ill. az eredeti hatszögben (3. ábra).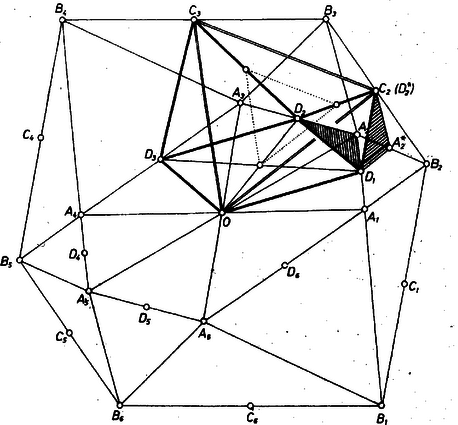

3. ábra

Egészítse ki a

D_{1}

D_{2}

D_{3}

pontokat paralelogrammává az

O

pont (

O

tehát

D_{2}

-nek a

D_{1} D_{3}

szakasz felezőpontjára vonatkozó tükörképe). Megmutatjuk, hogy a

C_{2} C_{3} O

háromszög szabályos, tehát

O

C_{1} C_{2} C_{3} C_{4} C_{5} C_{6}

szabályos hatszög középpontja, és így

O

helyzete nem függ attól, hogy melyik három felezőpontból származtatjuk. Feladatunk állítását ennek alapján már könnyen bebizonyíthatjuk.
Először azt mutatjuk meg, hogy a

D_{1} C_{2} D_{2}

háromszög szabályos. Feltehetjük, hogy az eredeti hatszög körüljárása pozitív. Forgassuk el a

D_{1} A_{2} D_{2}

háromszöget

D_{1}

körül negatív irányban

60^{\circ}

-kal. Az

A_{2}

D_{2}

csúcsok új helye legyen

A_{2}^{*}

D_{2}^{*}

. Ekkor a

D_{1} A_{2}^{*}

A_{2}^{*} D_{2}^{*}

szakaszok rendre párhuzamosak az

A_{1} B_{2}

A_{2} B_{3}

szakaszokkal és egyenlők azok felével,

D_{1} A_{2}^{*}

tehát az

A_{1} B_{2} A_{2}

háromszög középvonala,

A_{2}^{*} D_{2}^{*}

pedig a

B_{2} B_{3} A_{2}

háromszögé, azaz

C_{2}

és

D_{2}^{*}

azonosak:

D_{2}

-t a

D_{1}

körüli

60^{\circ}

-os forgatás

C_{2}

-be viszi,

D_{1} C_{2} D_{2}

tehát szabályos háromszög.
Azt bizonyítottuk be, hogy a csatlakozó

A_{1} A_{2}

és

A_{2} A_{3}

szakaszok

D_{1}

és

D_{2}

felezőpontja, és a szakaszok fölé rajzolt

A_{2} A_{1} B_{2}

és

A_{3} A_{2} B_{3}

szabályos háromszögek harmadik csúcsai által meghatározott

B_{2} B_{3}

szakasz

C_{2}

felezőpontja a

D_{2} D_{1} C_{2}

szabályos háromszöget határozza meg, ha

A_{2} A_{1} B_{2}

és

A_{3} A_{2} B_{3}

körüljárása megegyezik.
Eredményünkből következik, hogy a

D_{3} D_{2} C_{3}

háromszög is szabályos, és a

C_{2} D_{2}

D_{2} C_{3}

szakaszok fölé rajzolt

C_{2} D_{2} D_{1}

D_{2} C_{3} D_{3}

szabályos háromszögek

D_{1}

D_{3}

csúcsai által meghatározott szakasz felezőpontja a

D_{2} C_{2}

D_{2} C_{3}

szakaszok felezőpontjaival együtt szabályos háromszöget alkot. Ezt a háromszöget a

D_{2}

centrumból kétszeresére nagyítva épp az

O C_{2} C_{3}

háromszöget kapjuk, ez tehát szabályos háromszög.
Hasonló módon kapjuk, hogy a

D_{2}

D_{3}

D_{4}

csúcsokat paralelogrammává kiegészítő

O'

csúcs a

C_{3}

C_{4}

csúcsokkal együtt szabályos háromszöget alkot, ha tehát

C_{2}

C_{3}

C_{4}

egy szabályos hatszög csúcsai, akkor

O

és

O'

azonosak. A

D_{1} O

O D_{4}

szakaszok tehát párhuzamosak és egyenlők a

D_{2} D_{3}

szakasszal, és ez az utóbbi az

A_{2} A_{3} A_{4}

háromszög középvonala. A

D_{1} D_{4}

és

A_{2} A_{4}

szakaszok tehát párhuzamosak és egyenlők, így az

A_{1} A_{2} A_{4} A_{5}

négyszög paralelogramma (hiszen a

D_{1} D_{4}

középvonal párhuzamos és egyenlő az

A_{2} A_{4}

oldallal) és e paralelogramma centruma épp az

O

pont.
Hasonló módon láthatjuk be, hogy az eredeti hatszög további szemközti oldalpárjai is olyan paralelogramma oldalai, melynek középpontja a

C_{1} C_{2} C_{3} C_{4} C_{5} C_{6}

szabályos hatszög

O

centrumával azonos, az eredeti hatszög tehát centrálszimmetrikus.

Váli László (Budapest, I. István Gimn.)