Kezdőlap


Feladat:	Gy.2787	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Érik Róbert , Nagy Katalin , Németh Zoltán , Szőts Tímea , Valkó Benedek , Vörös Zoltán
Füzet:	1993/február, 71 - 72. oldal		PDF \| MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Szögfelező egyenes, Terület, felszín, Nevezetes egyenlőtlenségek, Gyakorlat
Hivatkozás(ok):	Feladatok: 1992/szeptember: Gy.2787

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük a háromszög oldalait $a$ , $b$ , $c$ -vel, magasságait a szokásos módon $m_{a}$ , $m_{b}$ , $m_{c}$ -vel, területét $T$ -vel. Világos, hogy $m_{a} \leq f_{a}$ , $m_{b} \leq f_{b}$ , $m_{c} \leq f_{c}$ és $2 T = a m_{a} = b m_{b} = c m_{c} = (a + b + c) r$ . Így

\begin{matrix} f_{a} + f_{b} + f_{c} \geq m_{a} + m_{b} + m_{c} = r (\frac{a + b + c}{a} + \frac{a + b + c}{b} + \frac{a + b + c}{c}), \end{matrix}

és itt

\begin{matrix} \frac{a + b + c}{a} + \frac{a + b + c}{b} + \frac{a + b + c}{c} = \\ = 3 + (\frac{a}{b} + \frac{b}{a}) + (\frac{a}{c} + \frac{c}{a}) + (\frac{b}{c} + \frac{c}{b}) \geq 3 + 3 \cdot 2 = 9. \end{matrix}

II. megoldás. Az Erdős‐Mordell egyenlőtlenség szerint (lásd. Reiman István: A geometria és határterületei, 230. old.), ha

P

belső pontja egy háromszögnek (1. ábra), akkor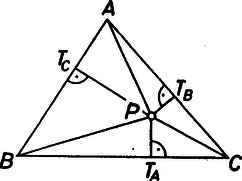

P A + P B + P C \geq 2 (P T_{A} + P T_{B} + P T_{C})

1. ábra

Speciálisan, ha

P

a beírt kör középpontja (2. ábra), akkor

\begin{matrix} P A + P B + P C \geq 6 r . \end{matrix}

2. ábra

P A^{'}

;

P B^{'}

;

P C^{'}

szakaszok mindegyike legalább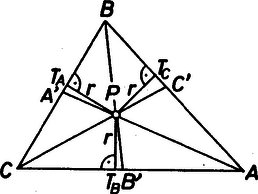

r

, ezért

\begin{matrix} f_{a} + f_{b} + f_{c} = P A + P A^{'} + P B + P B^{'} + P C + P C^{'} \geq 9 r . \end{matrix}