Kezdőlap


Feladat:	Gy.2715	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Csorba Zoltán , Dombi Gergely , Koblinger Egmont , Szeredi Tibor , Torma Péter
Füzet:	1992/november, 375 - 376. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Négyszögek geometriája, Gyakorlat
Hivatkozás(ok):	Feladatok: 1991/szeptember: Gy.2715

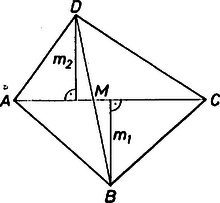
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük az $A B C D$ konvex négyszög átlóinak metszéspontját $M$ -mel, az $A B C$ háromszög és az $A C D$ háromszög $A C$ alaphoz tartozó magasságvonalát $m_{1}$ és $m_{2}$ -vel.

Ekkor

\begin{matrix} \frac{T_{M B A}}{T_{M B C}} = \frac{\frac{m_{1} \cdot A M}{2}}{\frac{m_{1} \cdot M C}{2}} = \frac{A M}{M C} \end{matrix}

és

\begin{matrix} \frac{T_{M D A}}{T_{M D C}} = \frac{\frac{m_{2} \cdot A M}{2}}{\frac{m_{2} \cdot M C}{2}} = \frac{A M}{M C} . \end{matrix}

Így

\begin{matrix} \frac{T_{M B A}}{T_{M B C}} = \frac{T_{M D A}}{T_{M D C}}, azaz T_{M B A} \cdot T_{M D C} = T_{M B C} \cdot T_{M D A} . \end{matrix}

(1)

Tegyük fel, hogy a

T_{A M B}

T_{B M C}

T_{C M D}

T_{D M A}

területek értékei

1

2

3

, illetve

4

valamilyen sorrendben. Ekkor az (1) összefüggés mindkét oldala egész szám, egyik oldalán

3

többszöröse áll, míg a másik oldal nem osztható

3

-mal. Ez nyilván nem lehet. Tehát nincs a feladat feltételeinek eleget tevő négyszög.