Kezdőlap


Feladat:	Gy.2707	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Balás Elemér , Csikai Szabolcs , Csorba Péter , Faragó Gergely , Galambos István , Gefferth András , Győrffy Werner , Kálmán Tamás , Kóczy László , Markót Mihály , Marx Gábor , Molnár-Sáska Gábor , Szántó András , Tichler Krisztián , Tomán Henrietta
Füzet:	1992/március, 112 - 113. oldal		PDF \| MathML
Témakör(ök):	Középpontos tükrözés, Paralelogrammák, Téglalapok, Síkgeometriai számítások trigonometria nélkül négyszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1991/május: Gy.2707

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A paralelogramma középpontosan szimmetrikus, ezért a szemközti csúcsokhoz tartozó belső szögfelezők egymás tükörképei, tehát párhuzamosak. Így az $E F G H$ négyszög is paralelogramma.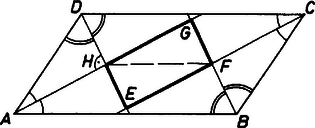

Továbbá

H A D ∢ + H D A ∢ = \frac{1}{2} (B A D ∢ + A B C ∢) = \frac{1}{2} \cdot 180^{\circ} = 90^{\circ}

, azaz

A H D ∢ = 180^{\circ} - (H A D ∢ + H D A ∢) = 90^{\circ}

. Tehát

E F G H

derékszögű paralelogramma, vagyis téglalap. A téglalap két átlója egyenlő hosszú, ezért elegendő pl. a

H F

átló hosszát meghatároznunk.
A

H

pont illeszkedik mind az

A

, mind a

D

csúcshoz tartozó belső szögfelezőre, ezért

H

egyenlő messze van az

A B

és az

A D

, valamint az

A D

és a

D C

oldalaktól, és így

H

rajta van a paralelogramma

A B

és

C D

oldalaival párhuzamos középvonalán. A szimmetria miatt ugyanez az

F

pontról is elmondható, ezért

H F ∥ C D

. Mivel azonban

H S ∥ F C

azért

H F C S

paralelogramma,

H F = S C = D C - D S

. Viszont

D S = D A

, mert a

D A S

háromszög egyenlő szárú, hiszen

D S A ∢ = S A B ∢

(váltószögek),

D A S ∢ = S A B ∢

(

A S

szögfelező). Tehát

H F = D C - D A

, vagyis az

E F G H

négyszög átlóinak hossza megegyezik az

A B C D

paralelogramma két szomszédos oldalának különbségével,

| a - b |

-vel.