Kezdőlap


Feladat:	Gy.2699	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Csorba Péter , Molnár-Sáska Gábor
Füzet:	1992/november, 374 - 375. oldal		PDF \| MathML
Témakör(ök):	Algebrai átalakítások, Geometriai egyenlőtlenségek, Derékszögű háromszögek geometriája, Téglalapok, Síkgeometriai számítások trigonometria nélkül, Gyakorlat
Hivatkozás(ok):	Feladatok: 1991/április: Gy.2699

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a téglalap oldalainak hosszát $a$ -val és $b$ -vel, az $a$ hosszúságú oldalak két végpontján átmenő és az előírás szerint érintő ‐ a szimmetria miatt nyilván egyenlő sugarú ‐ körök sugarát $r_{a}$ -val, a $b$ hosszúságú oldalak két végpontján átmenő körük sugarát pedig 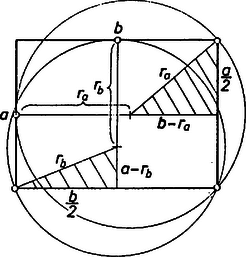$r_{b}$ -vel.

r_{a}

sugarú körök középpontja az egyik

a

hosszúságú oldaltól ‐ amelyet érint ‐

r_{a}

távolságra van, tehát a másik oldaltól

| b - r_{a} |

távolságra. Ezért Pitagorasz tétele szerint:

\begin{matrix} r_{a}^{2} = {(b - r_{a})}^{2} + {(\frac{a}{2})}^{2}, vagyis \\ r_{a} = \frac{4 b^{2} + a^{2}}{8 b} . \end{matrix}

Ugyanígy kapjuk, hogy

\begin{matrix} r_{b}^{2} = {(a - r_{b})}^{2} + {(\frac{b}{2})}^{2}, vagyis r_{b} = \frac{4 a^{2} + b^{2}}{8 a} . \end{matrix}

A bizonyítandó állítás tehát:

\begin{matrix} 2 \cdot \frac{4 b^{2} + a^{2}}{8 b} + 2 \cdot \frac{4 a^{2} + b^{2}}{8 a} \geq \frac{5}{8} (2 a + 2 b) . \end{matrix}

Megszorozva

4 a b > 0

-val és rendezve:

\begin{matrix} a^{3} + b^{3} - a^{2} b - b^{2} a \geq 0, azaz {(a - b)}^{2} (a + b) \geq 0 . \end{matrix}

Ez utóbbi egyenlőtlenség nyilván teljesül, s mivel ekvivalens eredeti állításunkkal, ezért az is igaz. Látható, hogy pontosan akkor van egyenlőség, ha

a = b

, azaz, ha a téglalap négyzet.