| Feladat: | Gy.2642 | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Megoldó(k): | Risbjerg Anna , Zsenei András | ||
| Füzet: | 1991/április, 161 - 162. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Kör (és részhalmaza), mint mértani hely, Mértani helyek, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1990/szeptember: Gy.2642 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Megoldás. A négyzet oldalegyenesei a síkot 9 részre osztják. Számozzuk meg a részeket az 1. ábrán látható módon. 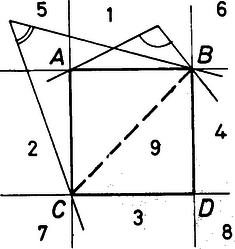 1. ábra Ha egy pont az 1.‐4. síkrészek valamelyikében helyezkedik el, akkor abból a négyzetnek valamelyik oldalát, ha pedig az 5.‐8. síkrészek valamelyikében, akkor abból a négyzetnek valamelyik átlóját látjuk. (Az 1. síkrészből például az oldalt, az 5. síkrészből pedig a átlót.) Tudjuk, hogy azon pontok mértani helye, melyekből egy szakasz adott szögben látszik, két, a szakaszra szimmetrikusan elhelyezkedő körív. Ezért feladatunk megoldását a négyzet oldalaihoz, illetve átlóihoz és az adott szöghöz tartozó látóköríveknek a megfelelő síkrészekbe eső részei adják. Ha az adott szög hegyesszög, akkor a körívek nagyobbak ugyan félkörnél, de pl. az szakaszhoz tartozó látókörívek közül csak az ívrész esik az 1. síkrészbe, tehát csak ez tartozik a mértani helyhez (2. ábra). 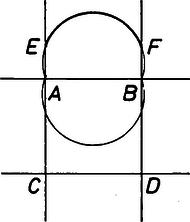 2. ábra Az oldalakhoz és az átlókhoz tartozó látókörívek a négyzet oldalainak meghosszabbításán csatlakoznak egymáshoz ezért a mértani hely egy, a 3. ábrán látható alakzat (8 ívdarab). 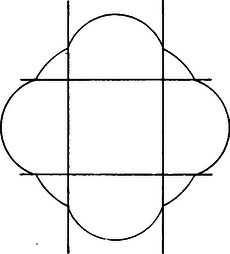 3. ábra Ha az adott szög hegyesszögnél nagyobb, akkor az átlók látókörívei a négyzet belsejében helyezkednek el, a mértani helynek az 5.‐8. síkrészekben nincs pontja. Ilyen esetben a keresett mértani hely a 4. ábrán látható négy körívből álló alakzat. 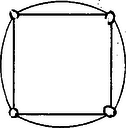 4. ábra Végül ha , úgy a négyzet csúcsai is a mértani helyhez tartoznak. |