Kezdőlap


Feladat:	Gy.2605	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Faragó Gergely , K. L.
Füzet:	1991/január, 17 - 18. oldal		PDF \| MathML
Témakör(ök):	Alakzatok hasonlósága, Beírt gömb, Térfogat, Térgeometriai számítások trigonometria nélkül, Tetraéderek, Gyakorlat
Hivatkozás(ok):	Feladatok: 1990/január: Gy.2605

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük a tetraéder csúcsait $A$ $B$ , $C$ , $D$ -vel, magasságvonalainak hosszát $m_{A}$ , $m_{B}$ , $m_{C}$ , $m_{D}$ -vel, a megfelelő lapok területét $T_{A}$ , $T_{B}$ , $T_{C}$ , $T_{D}$ -vel, a tetraéder térfogatát $V$ -vel, beírt gömbjének sugarát $ρ$ -val, a levágott kis tetraéderekbe írható gömbök sugarát pedig rendre $ρ_{A}$ , $ρ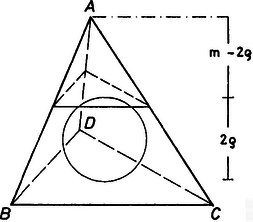_{B}$ , $ρ_{C}$ , $ρ_{D}$ -vel.

1. ábra

A levágott kis tetraéderek hasonlóak az eredeti tetraéderhez (1. ábra), mivel a párhuzamos szelők tétele szerint a két tetraéder közös csúcsából történő megfelelő arányú középpontos nagyítás a kis tetraédert átviszi a nagyba. Ezért a tetraéderekben a megfelelő szakaszok aránya megegyezik. A kis tetraéderek közös csúcshoz tartozó magassága megegyezik a nagy tetraéder megfelelő magasságának és a beírt gömb átmérőjének különbségével. A magasságok és a beírt gömb sugarának arányát felírva:

\begin{matrix} \frac{ρ_{A}}{ρ} = \frac{m_{A} - 2 ρ}{m_{A}}, \frac{ρ_{B}}{ρ} = \frac{m_{B} - 2 ρ}{m_{B}}, \frac{ρ_{C}}{ρ} = \frac{m_{C} - 2 ρ}{m_{C}}, \frac{ρ_{D}}{ρ} = \frac{m_{D} - 2 ρ}{m_{D}} . \end{matrix}

Ezeket rendezve és összeadva kapjuk, hogy:

\begin{matrix} ρ_{A} + ρ_{B} + ρ_{C} + ρ_{D} = 4 ρ - 2 ρ^{2} (\frac{1}{m_{A}} + \frac{1}{m_{B}} + \frac{1}{m_{C}} + \frac{1}{m_{D}}) . \end{matrix}

(1)

Tudjuk, hogy a tetraéder térfogatára fennáll, hogy

\begin{matrix} 3 V = T_{A} \cdot m_{A} = T_{B} \cdot m_{B} = T_{C} \cdot m_{C} = T_{D} \cdot m_{D} . \end{matrix}

Ebből

\begin{matrix} \frac{1}{m_{A}} + \frac{1}{m_{B}} + \frac{1}{m_{C}} + \frac{1}{m_{D}} = \frac{T_{A} + T_{B} + T_{C} + T_{D}}{3 V} . \end{matrix}

Ezt (1)-be helyettesítve:

\begin{matrix} ρ_{A} + ρ_{B} + ρ_{C} + ρ_{D} = 4 ρ - 2 ρ \cdot \frac{ρ (T_{A} + T_{B} + T_{C} + T_{D})}{3 V} . \end{matrix}

(2)

2. ábra

O

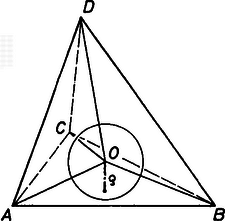a tetraéder beírt gömbjének a középpontja, akkor az

O A B C

tetraéder

O

-hoz tartozó magassága

ρ

(2. ábra), ezért a térfogata

\frac{T_{A}}{3} ρ

. A négy darab ilyen típusú egyenlőséget összeadva kapjuk, hogy

3 V = ρ T_{A} + ρ T_{B} + ρ T_{C} + ρ T_{D}

. Ezt (2)-be helyettesítve:

\begin{matrix} ρ_{A} + ρ_{B} + ρ_{C} + ρ_{D} = 4 ρ - 2 ρ = 2 ρ . \end{matrix}

A feladatban szereplő értékekkel

\begin{matrix} ρ = \frac{1}{2} (9 + 12 + 36 + 39) = 48 egység . \end{matrix}

Meg kell még vizsgálnunk, vajon létezik-e olyan tetraéder, amelynél a levágott kis tetraéderekbe írható gömbök sugarai

9,12,36,

és

39

egység. Megmutatható, hogy az a tetraéder, amelynek van három, egymásra páronként merőleges (közös csúcsból induló) éle, és ezek hossza rendre

128, 384

és

512

egység, éppen ilyen.

II. megoldás. Használjuk az I. megoldás jelöléseit, továbbá jelöljük az eredeti tetraéderhez hozzáírt gömbök sugarait rendre

ρ_{a}

ρ_{b}

ρ_{c}

ρ_{d}

-vel.
Ismert, (lásd pl. Geometriai feladatok gyűjteménye I., 2006/a feladat), hogy ekkor:

\begin{matrix} \frac{2}{ρ} = \frac{1}{ρ_{a}} + \frac{1}{ρ_{b}} + \frac{1}{ρ_{c}} + \frac{1}{ρ_{d}} . \end{matrix}

(3)

A levágott tetraéderek hozzáírt gömbje éppen az eredeti tetraéder beírt gömbje, ezért az I. megoldásban belátott hasonlóság miatt:

\begin{matrix} \frac{ρ_{A}}{ρ} = \frac{ρ}{ρ_{a}}, \frac{ρ_{B}}{ρ} = \frac{ρ}{ρ_{b}}, \frac{ρ_{C}}{ρ} = \frac{ρ}{ρ_{c}}, \frac{ρ_{D}}{ρ} = \frac{ρ}{ρ_{d}} . \end{matrix}

Ezekből

ρ_{a}, ρ_{b}, ρ_{c}

és

ρ_{d}

-t kifejezve, majd (

3

)-ba helyettesítve kapjuk, hogy:

\begin{matrix} \frac{2}{ρ} = \frac{ρ_{A} + ρ_{B} + ρ_{C} + ρ_{D}}{ρ^{2}}, \end{matrix}

azaz

\begin{matrix} ρ = \frac{ρ_{A} + ρ_{B} + ρ_{C} + ρ_{D}}{2} . \end{matrix}

Esetünkben tehát a beírt gömb sugara

\frac{9 + 12 + 36 + 39}{2} = 48 egység

Kassai Lóránt (Bp., Fazekas M. Gyak. Gimn., I. o. t.) dolgozata alapján