Kezdőlap


Feladat:	Gy.2579	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Csörnyei Mariann , Elek Cs. , Farkas Z. , Gefferth A. , K. L. , Molnár-Sáska G.
Füzet:	1990/április, 167 - 168. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Szinusztétel alkalmazása, Alakzatok köré írt kör, Gyakorlat
Hivatkozás(ok):	Feladatok: 1989/október: Gy.2579

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Először bebizonyítunk egy, a háromszög köré írt kör sugarára vonatkozó összefüggést:

(

*

) Tetszőleges háromszög köré írt körének sugarát megkaphatjuk úgy, hogy a háromszög két oldalának szorzatát elosztjuk a harmadik oldalhoz tartozó magasság kétszeresével.
Jelöljük az

A B C

háromszög szögeit és oldalait a szokásos módon. Legyen a köré írt kör középpontja

O

, sugara

R

, az

O C

egyenes és a köré írt kör másik metszéspontja

D

, a

B

csúcshoz tartozó magasság talppontja

T

, a magasságszakasz hossza pedig

m_{b}

. Azt kell megmutatnunk, hogy

R = \frac{a c}{2 m_{b}}

. Ha

α = 90^{\circ}

, akkor

c = m_{b}

, az állítás nyilvánvaló. Ha

α \neq 90^{\circ}

, akkor a

B D C

és a

T A B

háromszögek hasonlóak, mert

D B C ∢ = B T A ∢ = 90^{\circ}

, valamint a kerületi szögek tétele miatt

B D C ∢ = B A T ∢

. Ha

α < 90^{\circ}

, akkor mindkét szög a körülírt kör

B C

ívéhez tartozó kerületi szög (1/a ábra), ha pedig

α > 90^{\circ}

, akkor mindkét szög

180^{\circ}

-ra egészíti ki

α

-t (1/b ábr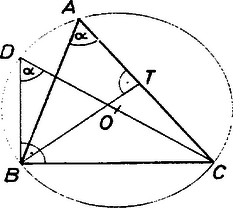a).

1/a ábra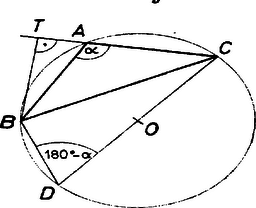

1/b ábra

Ezért a két háromszögben a megfelelő oldalak aránya is megegyezik, vagyis

\frac{B C}{D C} = \frac{B T}{B A}

, azaz

\frac{a}{2 R} = \frac{m_{b}}{c}

; rendezve:

\begin{matrix} R = \frac{a \cdot c}{2 m_{b}} . \end{matrix}

Térjünk vissza eredeti feladatunkra. Jelöljük a

P

pontnak a

B C

C A

illetve az

A B

oldalaktól való távolságát rendre

d_{a}

d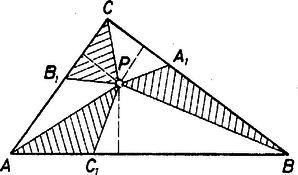_{b}

d_{c}

-ve1.

Alkalmazzuk a (

*

) állítást az

A C_{1} P

háromszögre. E háromszög

A C_{1}

oldalához tartozó magassága

d_{c}

, tehát a háromszög köré írható kör

R_{1}

sugarára:

R_{1} = \frac{A P \cdot P C_{1}}{2 d_{c}}

. Ugyanez a

d_{c}

magasság megtalálható a

C_{1} B P

háromszögben is, így e háromszög köré írható kör

R_{2}

sugarára:

R_{2} = \frac{P C_{1} \cdot B P}{2 d_{c}}

. Ugyanígy kifejezve a többi szereplő háromszög köré írt kör sugarát, bizonyítandó állításunk a következő alakot ölti:

\begin{matrix} \frac{A P \cdot P C_{1}}{2 d_{c}} \cdot \frac{B P \cdot P A_{1}}{2 d_{a}} \cdot \frac{C P \cdot P B_{1}}{2 d_{b}} = \\ = \frac{P C_{1} \cdot B P}{2 d_{c}} \cdot \frac{P A_{1} \cdot C P}{2 d_{a}} \cdot \frac{P B_{1} \cdot A P}{2 d_{b}} . \end{matrix}

Ez viszont nyilvánvaló azonosság.

Megjegyzések. 1. Teljesen hasonló módon látható be a feladat következő általánosítása: Legyen

P

A_{1} A_{2} ... A_{n}

konvex

n

-szög tetszőleges belső pontja,

B_{1}

B_{2}

...

B_{n}

pedig rendre az

A_{1} A_{2}

A_{2} A_{3}

...

A_{n} A_{1}

oldalak egy belső pontja. Ekkor az

A_{1} P B_{1}

A_{2} P B_{2}

...

A_{n} P B_{n}

háromszögek köré írt körök sugarainak szorzata megegyezik a

B_{1} P A_{2}

B_{2} P A_{3}

...

B_{n} P A_{1}

háromszögek köré írt körök sugarainak szorzatával.

Kassai Lóránt (Bp., Fazekas M. Gyak. Gimn., I. o. t.)

2. A (

*

) állítást sokan a szinusztétel segítségével bizonyították a következőképpen: A tétel szerint

R = \frac{a}{2 sin α}

. A törtet bővítve:

R = \frac{a b c}{2 b c sin α} = \frac{a b c}{4 T} = = \frac{a b c}{2 b \cdot m_{b}} = \frac{a c}{2 m_{b}}

(

T

a háromszög területe).