Kezdőlap


Feladat:	Gy.2538	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Balogh József , Harcos G. , Kovács T. , Podoski Károly , Tokodi T.
Füzet:	1989/november, 392 - 393. oldal		PDF \| MathML
Témakör(ök):	Tengelyes tükrözés, Trapézok, Diszkusszió, Körérintési szerkesztések, Síkgeometriai szerkesztések, Gyakorlat
Hivatkozás(ok):	Feladatok: 1989/február: Gy.2538

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tekintsük a feladatot megoldottnak. Állítsunk a $P$ pontban merőlegest a $C D$ oldalra, s tükrözzük erre az egyenesre $A$ -t; legyen a tükörkép $A''$ . Az $A$ pont $C D$ egyenesre vonatkozó tükörképe pedig legyen $A'$ . Mivel az $A$ pontot két egymásra merőleges tengelyre tükröztük, ezért a két tükörkép ‐ $A'$ és $A''$ ‐ valamint a tengelyek metszéspontja ‐ $P$ ‐ egy egyenesbe esik.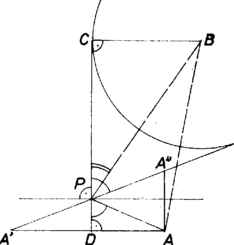

Feltételünk, valamint a tükrözés szögtartósága miatt

\begin{matrix} 2 B P C ∢ = A P D ∢ = A'' P C ∢, \end{matrix}

vagyis a

C P A''

szögnek a

B P

egyenes éppen a szögfelezője. A szögfelező pontjai a szög mindkét szárától egyenlő távolságra vannak. Mivel a

B C D

szög derékszög, ezért a

B

pont a

P A''

egyenestől is éppen

B C

távolságra van, azaz az

A' P A''

egyenes érinti a

B

középpontú,

B C

sugarú kört. Az érintő és a

C D

szakasz metszéspontja a keresett

P

pont. Ez a

P

pont nyilván eleget is tesz a feladat feltételeinek.
Ha

B C < C D

, akkor mindig 1 megoldás van (az

A'

pontból a körhöz húzható két érintő egyike nem a

C D

szakaszt, hanem annak

C

-n túli meghosszabbítását metszi), míg

B C ≧ C D

esetén nincs megoldás.

Balogh József (Szeged, JATE Ságvári E. Gyak. Gimn., III. o. t.)
dolgozata alapján