Kezdőlap


Feladat:	Gy.2508	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Nagy Judit
Füzet:	1989/március, 118 - 119. oldal		PDF \| MathML
Témakör(ök):	Tengelyes tükrözés, Pont körüli forgatás, Transzformációk fixpontjai, fixalakzatai, Transzformációk szorzata, Sokszögek szerkesztése, Gyakorlat
Hivatkozás(ok):	Feladatok: 1988/október: Gy.2508

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tekintsük a feladatot megoldottnak. A sokszög minden csúcsa rajta van a körön, tehát a sokszög minden oldalának felező merőlegese átmegy a kör középpontján. Jelöljük ezeket a felező merőlegeseket rendre $e_{1}, e_{2}, ..., e_{n}$ -nel. Ha a sokszögnek az 1. ábrán látható $A_{1}$ csúcsát $e_{1}$ -re tükrözzük, akkor az $A_{2}$ csúcsot kapjuk. Ezt tovább tükrözve $e_{2}$ -re $A_{3}$ -at kapjuk, és így tovább, $A_{i}$ -t $e_{i}$ -re tükrözve $A_{i + 1}$ -et kapjuk, míg végül $e_{n}$ -re való tükrözés után visszakapjuk az $A_{1}$ pontot. Tehát az $A_{1}$ fixpontja annak a transzformációnak, amely az $e_{1}, e_{2}, ..., e_{n}$ egyenesekre való tükrözések egymásutánjából áll. Vizsgáljuk meg, hogy ez a transzformáció milyen egyszerűbben leírható transzformációval helyettesíthető.

1. ábra

Ismert, hogy két egymást metsző tengelyre való tükrözés egymásutánja helyettesíthető egy, a tengelyek metszéspontja körüli elforgatással, melynek szöge éppen a tengelyek szögének a kétszerese (2. ábra).

2. ábra

Egy pont körüli elforgatás és egy, a ponton átmenő tengelyre való tükrözés egymásutánja pedig helyettesíthető egy olyan tengelyre való tükrözéssel, amelyik átmegy az adott ponton, és az eredeti tükrözés tengelyével feleakkora szöget zár be, mint az elforgatás szöge (3. ábra). (Ezeknek az állításoknak a bizonyítása megtalálható pl. Reiman István: Fejezetek az elemi geometriából c. középiskolai tankönyvének 33‐34. oldalán.)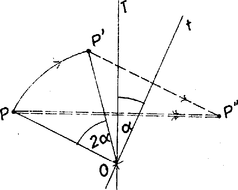

3. ábra

Jelöljük az

e_{i}

egyenesre való tükrözést

T_{i}

-vel, az adott kör

O

középpontja körüli

α

szögű elforgatást

F (α)

-val, az

e_{i}

és az

e_{j}

egyenesek szögét pedig

α_{i j}

-vel. Meg kell szerkesztenünk a

T_{1}, T_{2}, ..., T_{n} = T

transzformációnak az adott körvonalon levő fixpontjait.
Két esetet különböztetünk meg. Ha

n

páros, akkor

\begin{matrix} T = (T_{1} \cdot T_{2}) \cdot (T_{3} \cdot T_{4}) \cdot ... \cdot (T_{n - 1} \cdot T_{n}) = \\ F (2 α_{12}) \cdot F (2 α_{34}) \cdot ... \cdot F (2 α_{n - 1, n}) = F (2 (α_{12} + α_{34} + ... + α_{n - 1, n})) . \end{matrix}

Ez egy

O

körüli elforgatás, aminek csak akkor van

0

-tól különböző fixpontja, ha az elforgatás szöge

360^{\circ}

-nak egész számú többszöröse; akkor viszont minden pont fixpont.
Ha

n

páratlan, akkor

\begin{matrix} T = (T_{1} \cdot T_{2}) \cdot (T_{3} \cdot T_{4}) \cdot ... \cdot (T_{n - 2} \cdot T_{n - 1}) \cdot T_{n} = F (2 α_{12}) \cdot F (2 α_{34}) \cdot ... \cdot \\ \cdot F (2 α_{n - 2, n - 1}) \cdot T_{n} = F (2 (α_{12} + α_{34} + ... + α_{n - 2, n - 1})) \cdot T_{n} . \end{matrix}

Ez egy tengelyes tükrözés, aminek a körvonalon két fixpontja van.
Ezek alapján a szerkesztés a következőképpen végezhető el: Az

O

pontból merőlegeseket állítunk az adott egyenesekre, ezek éppen az

e_{i}

egyenesek lesznek. Ezután megszerkesztjük a

T

transzformációnak a körvonalon levő fixpontjait. Ha

n

páros, akkor

T

egy

O

körüli elforgatás, tehát vagy nincs fixpontja, azaz a feladatnak nincs megoldása (ha

2 (α_{12} + α_{34} + ... + α_{n - 1, n}) \neq k \cdot 360^{\circ})

, vagy végtelen sok fixpontja van (ha

2 (α_{12} + α_{34} + ... + α_{n - 1, n}) = k \cdot 360^{\circ})

), és ilyenkor a feladatnak is végtelen sok megoldása van, hiszen a körvonal tetszőleges

A_{1}

pontját sorban tükrözve az

e_{1}, e_{2}, ..., e_{n}

egyenesekre, a feltételeknek megfelelő (esetleg hurkolt) sokszöget kapunk. Ha

n

páratlan, akkor

T

egy tengelyes tükrözés, aminek a körön két fixpontja van; ekkor tehát két (

O

-ra tükrös helyzetű) megoldást kapunk úgy, hogy a fixpontot rendre tükrözzük az

e_{1}, e_{2}, ..., e_{n}

egyenesekre. Mivel az

n

darab egyenes sorrendje nem volt előírva, ezért a fenti eljárást az egyenesek minden lehetséges sorrendjében el kell végezni.

Nagy Judit (Miskolc, Földes F. Gimn., I. o. t.)
dolgozata alapján