Kezdőlap


Feladat:	Gy.2500	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Várady Péter
Füzet:	1989/március, 113 - 115. oldal		PDF \| MathML
Témakör(ök):	Egyéb sokszögek egybevágósága, Tengelyes tükrözés, Körülírt kör, Magasságpont, Paralelogrammák, Húrnégyszögek, Vektorok lineáris kombinációi, Gyakorlat
Hivatkozás(ok):	Feladatok: 1988/szeptember: Gy.2500

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Elegendő megmutatnunk, hogy a két négyszög megfelelő oldalai párhuzamosak és egyenlő hosszúak. Ez pontosan akkor teljesül, ha az $A B M_{A} M_{B}$ , $B C M_{B} M_{C}$ , $C D M_{C} M_{D}$ és $D A M_{D} M_{A}$ négyszögek paralelogrammák. A bizonyítást az 1. ábrán látható $A B M_{A} M_{B}$ négyszögre végezzük el, a többi négyszögre is lényegében ugyanaz a bizonyítás.

1. ábra

B M_{A}

és az

A M_{B}

egyenesek párhuzamosak, mert mindkettő merőleges a

C D

egyenesre ‐ mint a

B C D

, ill.

A C D

háromszög

C D

oldalához tartozó magassága. Tükrözzük az

M_{A}

és

M_{B}

pontokat a

C D

oldalra. Ismert, hogy az így kapott

M'_{A}

és

M'_{B}

tükörképek rajta vannak a

B C D

, illetve az

A C D

háromszög köré írt körön, ami esetünkben megegyezik a húrnégyszög köré írt körrel. Ezért a

B M'_{A} M'_{B} A

négyszög húrnégyszög. Viszont a

B M_{A}

és az

M_{A} M'_{A}

egyenesek egyaránt merőlegesek

C D

-re, ezért a

B M'_{A}

egyenes is merőleges

C D

-re, tehát a

B M'_{A} M'_{B} A

húrnégyszög két szemközti oldala párhuzamos, vagyis a négyszög szimmetrikus trapéz. Ha viszont egy szimmetrikus trapéz egyik szárát egy, az alapokra merőleges egyenesre tükrözzük, akkor a tükörkép párhuzamos a másik szárral. Ezért az

M_{A} M_{B}

egyenes mint az

M'_{A} M'_{B}

szár

C D

-re vonatkozó tükörképe ‐ párhuzamos az

A B

egyenessel. Vagyis az

A B M_{A} M_{B}

négyszög szemközti oldalai párhuzamosak, tehát a négyszög paralelogramma.
Ezzel a feladat állítását beláttuk.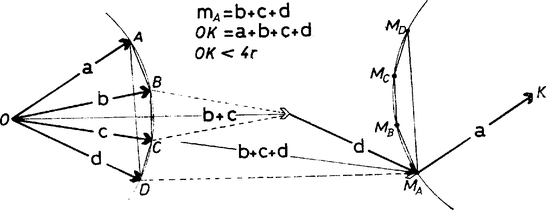

II. megoldás. Legyenek a húrnégyszög köré írt kör

O

középpontjából a csúcsokba mutató vektorok

a

b

c

d

, a magasságpontokba mutató vektorok pedig

m_{a}

m_{b}

m_{c}

m_{d}

. Ismeretes (l. pl. Geometriai feladatok gyűjteménye I., 3053. feladat) ‐ hogy minden háromszögben a körülírt kör középpontjából a csúcsokba mutató vektorok összege megegyezik a középpontból a magasságpontokba mutató vektorral. Esetünkben négy háromszögnek közös a körülírt köre, ezért:

\begin{matrix} m_{a} = b + c + d; m_{b} = a + c + d; m_{c} = a + b + d; m_{d} = a + b + c . \end{matrix}

Az eredeti négyszög oldalvektorai:

\begin{matrix} \vec{B A} = a - b, \vec{C B} = b - c, \vec{D C} = c - d és \vec{A D} = d - a . \end{matrix}

A magasságpontok által meghatározott négyszög oldalvektorai:

\begin{matrix} \vec{M_{A} M_{B}} = m_{b} - m_{a} = (a + c + d) - (b + c + d) = a - b = \vec{B A}, \end{matrix}

\begin{matrix} \vec{M_{B} M_{C}} = m_{c} - m_{b} = (a + b + d) - (a + c + d) = b - c = \vec{C B}, \end{matrix}

\begin{matrix} \vec{M_{C} M_{D}} = m_{d} - m_{c} = (a + b + c) - (a + b + d) = c - d = \vec{D C}, \end{matrix}

\begin{matrix} \vec{M_{D} M_{A}} = m_{a} - m_{d} = (b + c + d) - (a + b + c) = d - a = \vec{A D} . \end{matrix}

2. ábra

Tehát a húrnégyszög oldalvektorai rendre megegyeznek a magasságpontok által alkotott négyszög oldalvektoraival. Ebből pedig következik, hogy a két négyszög egybevágó.

Várady Péter (Győr, Révai M. Gimn., I. o. t.)
dolgozata alapján