Kezdőlap


Feladat:	Gy.2491	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1989/február, 71 - 73. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Algebrai átalakítások, Tengelyes tükrözés, Szögfelező egyenes, Gyakorlat
Hivatkozás(ok):	Feladatok: 1988/május: Gy.2491

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Azt mutatjuk meg, hogy a $P$ ponton átmenő, a szög szárait metsző tetszőleges egyenes által a szárakból levágott szakaszok reciprokainak összege megegyezik a $P$ -ben a szög felezőjére állított merőleges által a szögszárakból lemetszett két ‐ egyenlő hosszú ‐ szakasz reciprokának összegével. (Ebből feladatunk állítása nyilván következik.)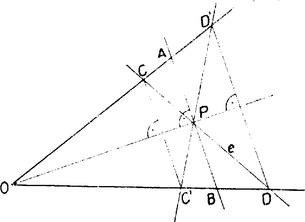
Jelöljük a szög csúcsát $O$ -val, $P$ -ben a szögfelezőre állított merőleges és a szögszárak metszéspontját $A$ -val, illetve $B$ -vel, a $P$ -n átmenő tetszőleges $e$ egyenesnek a szárakkal való metszéspontját $C$ -vel, illetve $D$ -vel, végül az $e$ egyenes szögfelezőre vonatkozó tükörképének a szárakkal való metszéspontját $C'$ -vel, illetve $D'$ -vel (1. ábra).

1. ábra

Ekkor a bizonyítandó állítás a következő:

\begin{matrix} \frac{1}{O C} + \frac{1}{O D} = \frac{2}{O A} . \end{matrix}

(1)

C C'

A B

D D'

egyenesek párhuzamosak, mivel a tükrözés miatt mindegyikük merőleges a szögfelezőre. Ezért az

O C C'

O A B

és

O D D'

háromszögek hasonlóak, így megfelelő oldalaik aránya megegyezik:

\begin{matrix} \frac{C C'}{O C} = \frac{A B}{O A} = \frac{D D'}{O D} . \end{matrix}

Ebből

\frac{1}{O A}

és

\frac{1}{O D}

értékét kifejezve, majd (1)-be helyettesítve:

\begin{matrix} \frac{1}{O C} + \frac{1}{O C} \cdot \frac{C C'}{D D'} = \frac{2}{O C} \cdot \frac{C C'}{A B}; \end{matrix}

rendezve:

\begin{matrix} C C' - \frac{D D'}{C C' + D D'} = \frac{A B}{2} . \end{matrix}

(2)

C C' P

és

D D' P

háromszögek is hasonlók, mert megfelelő szögeik egyenlők; ezért:

\begin{matrix} \frac{C C' + D D'}{D D'} = \frac{C C'}{D D'} + 1 = \frac{C P}{P D} + 1 = \frac{C P + P D}{P D} = \frac{C D}{P D}, \end{matrix}

azaz

\begin{matrix} \frac{D D'}{C C' + D D'} = \frac{P D}{C D} . \end{matrix}

Ezt írjuk be (2)-be:

\begin{matrix} C C' \cdot \frac{P D}{C D} = \frac{A B}{2}, \end{matrix}

vagyis

A B = 2 P B

miatt:

\begin{matrix} \frac{C C'}{C D} = \frac{P B}{P D} . \end{matrix}

(3)

Ez valóban igaz, hiszen a

C C' D

és a

P B D

háromszögek is párhuzamosan hasonlóak, következésképpen megfelelő oldalaik aránya megegyezik. Mivel átalakításaink megfordíthatók, azért (3) teljesülése azt jelenti, hogy a bizonyítandó (1) állítás is igaz.

II. megoldás. Ismert, hogy egy háromszög

c

oldalához tartozó szögfelezőjének: hossza (a szokásos jelöléseket alkalmazva)

\begin{matrix} f_{c} = \frac{2 a b cos \frac{γ}{2}}{a + b} . \end{matrix}

Ekkor ‐ a 2. ábra jelöléseivel ‐ az

O P

szakasz az

O A_{1} B_{1}

és az

O A_{2} B_{2}

háromszögben egyaránt szögfelező, tehát

\begin{matrix} O P = \frac{2 a_{1} b_{1} \cdot cos \frac{γ}{2}}{a_{1} + b_{1}} = \frac{2 a_{2} b_{2} cos \frac{γ}{2}}{a_{2} + b_{2}} . \end{matrix}

A második egyenlőség mindkét oldalát eloszthatjuk

2 \cdot cos \frac{y}{2}

-vel; ezután rendezéssel a kívánt összefüggéshez juthatunk.

2. ábra

Megjegyzés. Az első megoldás második részében lényegében azt az ismert összefüggést bizonyítottuk be, hogy egy trapéz átlóinak metszéspontján átmenő, az alapokkal párhuzamos egyenesnek a trapéz belsejébe eső szakasza éppen a két alap harmonikus közepe.