Feladat: Gy.2490 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Balogh József 
Füzet: 1989/február, 69 - 71. oldal  PDF  |  MathML 
Témakör(ök): Geometriai egyenlőtlenségek, Derékszögű háromszögek geometriája, Magasságvonal, Beírt kör, Indirekt bizonyítási mód, Hossz, kerület, Terület, felszín, Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat
Hivatkozás(ok):Feladatok: 1988/május: Gy.2490

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen az ABC derékszögű háromszög beírt körének középpontja O, a beírt körnek az oldalakon levő érintési pontjai pedig X, Y és Z (1. á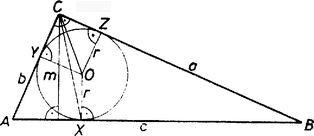bra).

 
 
1. ábra
 

Ekkor a CYOZ négyszögben OY=OZ=r, továbbá YCZ∢=CZO∢=CYO∢=90∘ (a két utóbbi szög a kör érintőjének az érintési pontba húzott sugárral bezárt szöge), tehát a CYOZ négyszög négyzet. Ezért CO=r2. A CX távolság legalább akkora, mint az ABC háromszög C csúcshoz tartozó magassága, azaz m. Másrészt a COX (esetleg elfajuló) háromszögben a háromszög‐egyenlőtlenség szerint: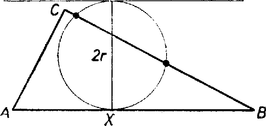
m≦CX≦CO+OX=r2+r.
Ezt rendezve :
rm≧12+1=2-1>0,4.
Ezzel a bizonyítandó állítás egyik felét beláttuk.
 
 
2. ábra
 

Tegyük fel, hogy van olyan háromszög, amelyben ‐ a bizonyítandó állítás második felével ellentétben ‐ r≧0,5m. Tekintsük a beírt körnek az AB oldallal párhuzamos másik érintőjét. Feltevésünk szerint a C csúcs az érintőegyenes és az AB oldal közti sávban helyezkedik el (2. ábra). Feltehetjük, hogy a C pont az AB szakaszra X-ben emelt merőlegesnek például a B-t nem tartalmazó oldalán van. Ekkor viszont a CB szakasz nem érintheti a beírt kört, ami ellentmondás. Tehát hibás az eredeti feltevésünk, vagyis rm<0,5. (A bizonyítás második felében nem használtuk ki, hogy a C csúcsnál derékszög van, tehát tetszőleges háromszög tetszőleges magasságára igaz, hogy rm<0,5.)
Ezzel a feladat állítását beláttuk.
 

II. megoldás. Az rm hányados értékét kifejezhetjük a háromszög oldalaival. Írjuk fel az ABC háromszög területét kétféleképpen ‐ az 1. ábra jelöléseit használva ‐ egyrészt úgy, mint az AOB, BOC és COA háromszögek területének összege, másrészt mint az AB oldal és a hozzá tartozó magasság szorzatának fele:
T=12c⋅r+12a⋅r+12b⋅r=12⋅c⋅m;
ebből
rm=ca+b+c.
Így a feladatot visszavezettük a derékszögű háromszög oldalaira vonatkozó egyenlőtlenségekre. Először azt mutatjuk meg, hogy ca+b+c<0,5. Ezt rendezve: c<0,5(a+b+c), azaz 0,5c<0,5(a+b), ami valóban igaz a háromszög‐egyenlőtlenség miatt. (Most sem használtuk ki, hogy az ABC háromszög derékszögű.)
 

A másik egyenlőtlenség helyett ezúttal is az erősebb 2-1≦ca+b+c egyenlőtlenséget bizonyítjuk. Azt kell megmutatnunk, hogy:
12+1≦ca+b+c=1a+bc+1.

Mivel pozitív számokról van szó, ezért ez ekvivalens a következővel:
a+bc+1≦2+1,azaza+b≦c⋅2.
Emeljük itt mindkét oldalt négyzetre (ez is ekvivalens átalakítás, hiszen a szóban forgó számok pozitívak). Pitagorasz tételét alkalmazva:
(a+b)2≦2c2=2a2+2b2,
azaz
0≦a2+b2-2ab=(a-b)2.
Ez valóban teljesül, s mivel ekvivalens átalakításokat végeztünk, ezért a bizonyítandó egyenlőtlenség is igaz.
 

 Balogh József (Szeged, JATE Ságvári E. Gyak. Gimn., II. o. t.)
 megoldása alapján
 

Megjegyzés. Belátható, hogy az rm hányados értéke 0,5-et tetszőlegesen megközelítheti, de soha nem éri el. Alulról viszont felveszi a 2-1 értéket, ha a derékszögű háromszög egyenlő szárú.