Kezdőlap


Feladat:	Gy.2489	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1989/január, 23 - 24. oldal		PDF \| MathML
Témakör(ök):	Algebrai átalakítások, Kombinatorikai leszámolási problémák, Számsorozatok, Gyakorlat
Hivatkozás(ok):	Feladatok: 1988/május: Gy.2489

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Megmutatjuk, hogy a kérdéses összeg minden szóba jövő ${a_{n}}$ sorozatra ugyanakkora. Először is jegyezzük meg, hogy $a_{19} = 88$ miatt a $b_{1}, b_{2}, ..., b_{88}$ értékek léteznek és mindegyikük ‐ természetesen ‐ legfeljebb 19.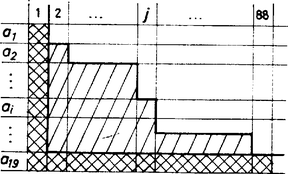

Készítsük el az ábrán látható

19 \times 88

-as táblázatot. A táblázat

i

-edik sorának

j

-edik mezőjét fessük feketére, ha

j \leq a_{i}

, egyébként ez a mező maradjon fehér.
Az

i

-edik sorban ekkor nyilván

a_{i}

darab fekete mező van, a táblázatban tehát összesen

\begin{matrix} a_{1} + a_{2} + ... + a_{19} \end{matrix}

mezőt festettünk feketére.
A fehér mezőket oszloponként számoljuk össze. A

j

-edik oszlopban a

j

-nél kisebb

a_{i}

-k soraiban álló mezők maradtak fehéren; ezek száma pontosan annyi, ahány

j

-nél kisebb eleme van az

a_{n}

sorozatnak, azaz

{b_{n}}

értelmezése szerint ‐ éppen

b_{j} - 1

darab. Fehér mező tehát összesen

\begin{matrix} (b_{1} - 1) + (b_{2} - 1) + ... + (b_{88} - 1) \end{matrix}

maradt a táblázatban.
A

19 \times 88

mező mindegyike vagy fekete, vagy fehér, így a vizsgált összeg értéke

\begin{matrix} 19 \cdot 88 + 88 = 1760 \end{matrix}

minden olyan monoton

a_{n}

sorozatra, melyre

a_{19} = 88

II. megoldás. A

{b_{n}}

sorozat értelmezése miatt az

{a_{n}}

sorozatnak

b_{m} - 1

darab

m

-nél kisebb eleme van, így

(b_{m + 1} - 1) - (b_{m} - 1) = b_{m + 1} - b_{m}

olyan eleme, ami éppen

m

.
A feltétel szerint

a_{19} = 88

, ezért a 88 nyilván

(20 - b_{88})

-szor fordul elő. Ez azt jelenti, hogy

\begin{matrix} a_{1} + a_{2} + ... + a_{19} = \\ = (b_{2} - b_{1}) \cdot 1 + (b_{3} - b_{2}) \cdot 2 + ... + (b_{88} - b_{87}) \cdot 87 + (20 - b_{88}) \cdot 88 = \\ = 20 \cdot 88 - (b_{1} + b_{2} + ... + b_{88}), és így a_{1} + a_{2} + ... + a_{19} + b_{1} + b_{2} + ... + b_{88} = \\ = 20 \cdot 88 = 1760. \end{matrix}