Feladat: Gy.2427 Korcsoport: 16-17 Nehézségi fok: nehéz
Füzet: 1988/március, 115 - 118. oldal  PDF  |  MathML 
Témakör(ök): Egyéb szinezési problémák, Osztópontok koordinátái, Terület, felszín, Négyszögek középvonalai, Négyszögek geometriája, Helyvektorok, Vektorok, Gyakorlat
Hivatkozás(ok):Feladatok: 1987/szeptember: Gy.2427

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladat állítása jóval általánosabb körülmények között is igaz. Osszuk ugyanis a négyszög szemközti AB és CD, illetve BC és AD oldalait 2n, illetve 2m ‐ tehát mindkét esetben páros sok ‐ egyenlő részre. (A feladatban n=m=4.) Ha most a szemközti oldalak megfelelő osztópontjait összekötő szakaszok révén nyert felosztás összesen 4mn darab kis négyszögét színezzük ki sakktáblaszerűen, akkor továbbra is igaz, hogy a fekete négyszögek területének összege egyenlő a fehérekével.

 
 
1. ábra
 

A bizonyítás során az alábbi két segédtételt használjuk fel:
1. Egy konvex négyszöget a két középvonala négy olyan négyszögre oszt, melyek közül a két-két szemközti területének az összege egyenlő (1. ábra). (Ez éppen a feladat állítása az n=m=1 esetben.)
2. Ha egy konvex négyszög szemközti oldalait k-k, illetve l-l egyenlő részre osztjuk (k≧2, l≧2), akkor a megfelelő osztópontokat összekötő szakaszokat ugyancsak egyenlő részekre osztják a létrejövő metszéspontok (2. ábra).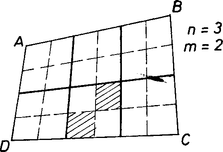
 
 
2. ábra
 

 
 
3. ábra
 

A fentiek felhasználásával már könnyen adódik a bizonyítandó állítás. A páros sorszámú osztóvonalak ugyanis n⋅m darab olyan négyszögre osztják az eredeti négyszöget, amelyekben a páratlan sorszámú osztóvonalak a 2. segédtétel szerint középvonalak (3. ábra). A fekete és fehér négyszögek területének összege tehát az 1. segédtétel szerint külön-külön egyenlő az n⋅m darab "kétszer kettes'' négyszög mindegyikében. Ekkor pedig nyilván az eredeti ABCD négyszögben is egyenlő a szóban forgó területek összege.
Ami a felhasznált segédtételeket illeti, az elsőnek a bizonyítása leolvasható a 4. ábráról. (A súlyvonal felezi a háromszög területét, így az egyenlő számokkal jelölt háromszögek területe egyenlő.)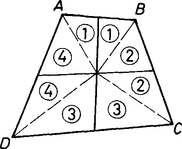
 
 
4. ábra
 

 
 
5. ábra
 

A 2. segédtételt az alábbi, kissé általánosabb alakban látjuk be:
 

2'. Ha az eredeti ABCD négyszög oldalain az 5. ábra szerint fölvett E és G, illetve F és H pontok külön-külön azonos arányban osztják a négyszög két-két szemközti oldalát, tehát
AEEB=DGGC=αβésBFFC=AHHD=λμ,
akkor a szemközti oldalak megfelelő osztópontjait összekötő szakaszok M metszéspontja is ezen arányokban osztja a rajta áthaladó osztóvonalakat, vagyis
HMMF=αβésEMMG=λμ.

Vektorokat használva egyszerű számolással adódik a 2'. állítás. Ha ugyanis a tér egy rögzített O pontjából a négyszög csúcsaihoz vezető helyvektorok és az adott paraméterek (α, β, λ, μ) segítségével felírjuk a HF szakaszt α:β arányban osztó M1 és az EG szakaszt λ:μ arányban osztó M2 pontokba mutató helyvektorokat, akkor kiderül, hogy a két vektor egyenlő, és így M1=M2=M, vagyis az M pont mindkét osztóvonalat a kívánt arányban osztja.
Az egyes pontok helyvektorait a megfelelő kisbetűvel jelölve:
m1=αf+βhα+β=αλc+μbλ+μ+βλd+μaλ+μα+β.(1)
Az m1, f és h vektorok felbontásakor felhasználtuk azt az ismert tényt, hogy szakasz adott (u:v) arányú osztópontjába mutató helyvektor a 6. ábrán látható módon fejezhető ki a végpontokba mutató helyvektorok segítségével.
 
 
6. ábra
 

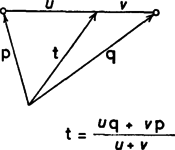Az (1) jobb oldalán álló kifejezés tagjait a vektorok számmal való szorzásának műveleti tulajdonságai szerint csoportosítva:
m1=λαc+βbα+β+μαb+βaα+βλ+μ=λg+μeλ+μ=m2
és éppen ezt akartuk bizonyítani.
 

Megjegyzés. A bizonyítás során a 2. segédtételben kimondott tény teszi lehetővé az 1. állítás alkalmazását. Ennek igazolása, tehát hogy az egyes osztóvonalakon is egyenlő hosszú szakaszok jönnek létre, a feladat eredetileg kitűzött formájában sem hagyható el. Elvégezhető viszont vektorok nélkül is, bár a közölt bizonyítás jól mutatja használatuk előnyeit.
Egy másik ‐ bár eléggé hosszadalmas ‐ bizonyítási lehetőség, ha a négyszög oldalfelező pontjaiból kiindulva a kerületen levő szakaszok ismételt felezésével jutunk el a feladatban szereplő vonalrendszerig, miközben az ABCD négyszög belsejében létrejövő metszéspontok vizsgálata során újra és újra fölhasználjuk, hogy tetszőleges négyszög középvonalai felezik egymást. A 2. állítást így csak a k=l=2n esetekre láthatjuk be, ami persze a kitűzött feladat megoldásához elegendő.
Az alábbiakban vázoljuk a 2. állításnak a k+l értéke szerinti teljes indukcióval történő bizonyítását. Mivel k,l≧2, ezért k+l≧4. Ha k+l≧4, akkor k=l=2, és az állítás azt mondja, hogy egy négyszög középvonalai felezik egymást.
Legyen most k+l>4, és tegyük fel, hogy a 2. állítás igaz a négyszög kerületének minden olyan k', l' felosztására, ahol k'+l'<k+l. Hívjuk az AB és CD osztópontjait összekötő k-1 darab osztóvonalat "függőlegesnek'', a további l-1 darabot pedig "vízszintesnek''. Mivel k+l>4, föltehető, hogy l≧3. Ekkor különbözők az AB-hez, illetve CD-hez legközelebb haladó vízszintes osztóvonalak, az A'B' és a C'D' (7. ábra).
 
 
7. ábra
 

Osszuk az A'B' és a C'D' szakaszokat k-k darab egyenlő részre (a 7. ábrán fehér pontok). Ekkor az indukciós feltevés alkalmazható az A'B'CD és az ABC'D' (valódi) négyszögekre. Eszerint az A'B'CD függőleges osztóvonalai a C'D', az ABC'D' függőleges osztóvonalai pedig az A'B' szakaszt osztják k-k egyenlő részre. A megfelelő függőleges osztóvonalak tehát azonosak a két résznégyszögben, hiszen a különböző A'B' és C'D' szakaszok megfelelő osztópontjait kötik össze. Ezek a vonalak tehát éppen az ABCD négyszög függőleges osztóvonalai, amelyek az A'B' és C'D' osztóvonalakat a fehér pontok fölvétele, a további vízszintes osztóvonalakat pedig az indukciós feltevés miatt osztják egyenlő szakaszokra.
Ami a függőleges osztóvonalak felosztását illeti, az indukciós feltevés szerint ezek AB és C'D', illetve A'B' és CD közé eső szakaszait egyaránt l-1(≧2) egyenlő részre osztják a vízszintes osztóvonalak. Mivel l≧3, a két "szélső'' részhez van olyan, amelyik mindkettejükkel egyenlő, tehát végül is mind az l darab szakasz ugyanolyan hosszú a függőleges osztóvonalakon. Ezzel a bizonyítást befejeztük.