| Feladat: | Gy.2420 | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Benkő D. , Csirik J. , Csordás Z. , Károlyi A. , Somfai E. | ||
| Füzet: | 1988/január, 23 - 27. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Geometriai egyenlőtlenségek, Egyéb ponthalmazok a koordinátasíkon, Alakzatok mértéke, Ellipszis, mint kúpszelet, Hiperbola, mint kúpszelet, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1987/május: Gy.2420 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Két pont "régi távolságát'' az egybevágósági transzformációk (pl. eltolás, elforgatás, tengelyes tükrözés) változatlanul hagyják, vagyis ha a és pontok képe és , akkor . Ezért ha a feladat a régi távolságra vonatkozna, akkor a és pontokat bárhogyan elhelyezhetnénk a koordináta-rendszerben, például az ilyenkor szokásos módon úgy, hogy illeszkedjenek az tengelyre, felezőpontjuk pedig az origó legyen. A feladatban definiált új távolság azonban függ a pontoknak a koordináta-rendszerben való elhelyezésétől. Tekintsük ugyanis például a és a pontokat. Ezek új távolsága . Ha elforgatjuk a pont körül a pontot úgy, hogy a pontba kerüljön (1. ábra), akkor a képpontok új távolsága . 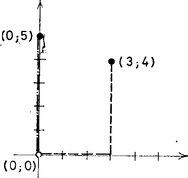 Vannak azonban olyan transzformációk, amelyek nem változtatják meg az új távolságot sem. Ilyen egy vektorral való eltolás. Ekkor a képe , a képe , és a képpontok új távolsága egyenlő a és új távolságával, hiszen Ugyanígy nem változtatja meg az új távolságot az vagy az tengelyre vonatkozó tükrözés sem. Ezeknél képe , illetve . Feltehetjük tehát, hogy a koordináta-rendszer origója a két adott pontot összekötő szakasz felezőpontja (ha nem, akkor egy "új távolság''-tartó eltolással odavisszük), az egyik adott pont pedig az I. síknegyedben van (ha nem, akkor tükrözzük az vagy az tengelyre, esetleg mindkettőre). Legyenek tehát az adott "fókuszpontok'' és , ahol és , az adott állandó pedig . Az pont pontosan akkor van rajta az új ellipszisen, ha
 Ez az egyenlet kilenc különböző egyenletre bomlik aszerint, hogy milyen az egyes abszolút értékekben lévő mennyiségek előjele, vagyis hogy az pont a 2. ábrán a szaggatott vonalak ‐ az , , , egyenletű egyenesek ‐ által határolt kilenc síkrész közül melyikben helyezkedik el. Ha vagy értéke , akkor a részek száma hatra csökken ‐ a függőleges vagy a vízszintes "középső réteg'' az , illetve az tengellyé egyszerűsödik ‐ ha pedig , azaz a két pont, és azonos, akkor a tengelyek határolta négy síknegyed marad. Nyilván
 A 2. ábrán satírozott "középső'' tartomány kivételével egyenesek ‐ mégpedig részint a tengelyekkel, részint azok szögfelezőivel párhuzamos egyenesek ‐ egyenleteit kaptuk, így az új ellipszisnek a ‐ legfeljebb ‐ nyolc nem korlátos tartományba eső része a megfelelő egyenletű egyenes ide eső szakasza. Látható, hogy mind a nyolc egyenesnek ugyanakkor ‐ a esetben ‐ van pontja a megfelelő tartományok belsejében. Ekkor a "középső'' tartományon természetesen nem teljesül a feltétel, így ha , akkor az új ellipszis egy ‐ a vagy esetben elfajuló ‐ nyolcszög (4. ábra, , ). Ha például , akkor a nyolcszögnek az tengellyel párhuzamos oldalai egyetlen ponttá zsugorodnak (5. ábra, , , ), és így hatszöget kapunk, ha pedig , akkor ugyanez történik az tengellyel párhuzamos oldalakkal is (6. ábra, , ), az új ellipszis négyzet. (A két adott pont ilyenkor egybeesik, tehát ebben a speciális esetben adott ponttól adott "új távolságra'' levő pontok halmazával, új körrel állunk szemben.) 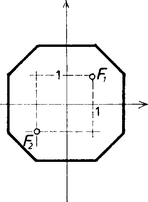 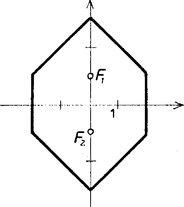 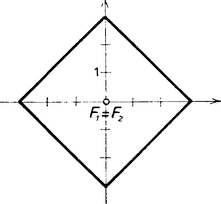 Ha , akkor a 2. ábra satírozott középső téglalapját kapjuk a határoló szakaszokkal együtt. Az új ellipszis tehát most egy zárt téglalap pontjaiból áll, ami az elfajuló esetekben szakasszá, illetve ponttá zsugorodik. Végül ha , tehát a fókuszok új távolsága nagyobb, mint a megadott állandó, akkor egyetlen tartományon sem teljesül a talált egyenlet, így ilyenkor nincs pontja az új ellipszisnek. Az új hiperbolák vizsgálata hasonló, bár a fentinél bonyolultabb esetvizsgálattal jár. Az , pontok megfelelő fölvételekor tegyük föl azt is, hogy ‐ ez nyilván megtehető. Ezután a pont akkor és csak akkor illeszkedik az új hiperbolára, ha
Most az alábbi egyenlőségekre van szükségünk :
A "belső'' abszolútértékek vizsgálatakor most is a 2. ábra tartományai adódnak. A kilenc lehetőséget a 7. ábra táblázata foglalja össze. (Zárójelben most is az egyenletek bal oldalára a megfelelő tartományokon fennálló egyenlőtlenségek állnak, és a könnyebb hivatkozás céljából megszámoztuk az egyes tartományokat.) Hívjuk még az 5. tartományt az új hiperbola főtéglalapjának.  Látható, hogy most a esetben nincs pontja az új hiperbolának, tehát itt az szükséges, hogy a megadott állandó ne legyen nagyobb, mint a fókuszok új távolsága. Most az 1. és 4., illetve a 2. és 3. tartományokon kapott feltételek nem függenek -től és -tól, így ezek a síknegyedpárok vagy teljes egészükben hozzátartoznak az új hiperbolához, vagy egyetlen pontjuk sem. A föltevés miatt az 1. és a 4. tartományban az abszolútérték jelek elhagyhatók, a 6. és 7. tartományban pedig csak , illetve formában bonthatók fel, hiszen a 6. és a 7. tartományon , és így az , illetve az egyenletű egyenesek az elfajuló esetek kivételével e tartományokon kívül haladnak. Még így is sokkal változatosabb alakzatokhoz juthatunk, mint az előbb, hiszen a "középső'' három tartományon (5., 8., 9.) két-két egyenes egyenlete adódik ‐ ha , akkor ezek páronként egybeesnek ‐ az pedig a paraméterek (, és ) viszonyától függ, hogy ezek az egyenesek hogyan helyezkednek el a megfelelő tartományokhoz képest. Az új hiperbolának a főtéglalap határára eső pontjait nyilván az adott oldallal szomszédos mindkét tartomány pontjaként megkaphatjuk, így az új hiperbolának a főtéglalap belsejében haladó szakaszai ‐ az és az egyenletű egyenesek ide eső részei ‐ éppen a szomszédos tartományokban (6., 7., 8., 9.) haladó félegyenes vagy félegyenesek kezdőpontjában metszik ennek a téglalapnak a kerületét. Kivételt jelent, ha az egyenletű egyenespár a főtéglalap két átellenes csúcsán halad át ‐ ha vagy ‐ ilyenkor ugyanis az új hiperbolához a szóban forgó csúcspárra illeszkedő negyedsíkok ‐ 1. és 4., illetve 2. és 3. tartományok ‐ tartoznak.  Mármost a föltevés mellett a főtéglalap és az egyenletű egyenespár viszonyát az határozza meg, hogy a intervallumhoz képest hol helyezkedik el az . A 8. ábrán ‐ ahol a középpontos szimmetria miatt csak az egyenletű egyenes lehetséges helyzeteit rajzoltuk meg ‐ az , , , , típusú elhelyezkedésekre rendre az , , , , esetekben kerül sor. Így kapjuk a hátsó borító ábráit, és ezzel az új hiperbola típusait, míg a 9. ábra az elfajult típusokat mutatja. Ezzel a megoldást befejeztük.  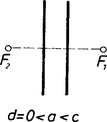 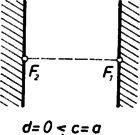 Megjegyzés. Ha jelöli a és pontok új távolságát, akkor, mint láttuk, új ellipszisben  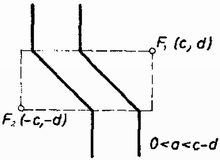 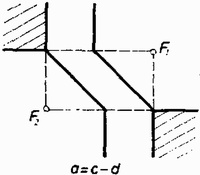 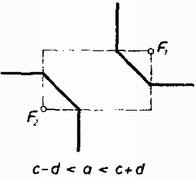 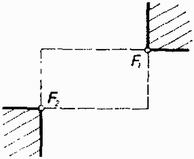 |