| Feladat: | Gy.2389 | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Bánkövi Johanna , Beke T. , Benczúr A. , Bereczky Á. , Cynolter G. , Fleiner T. , Hajnal Z. , Károlyi Enikő , Keleti T. , Majoros L. , Rimányi R. , Sustik M. , Szabó 484 P. , Szabó 639 A. , Szalay Gy. , Szederkényi Judit , Varga Zs. , Vasy A. , Zaránd G. | ||
| Füzet: | 1987/október, 296 - 298. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Alakzatok egybevágósága, Gömbi geometria, Szélsőérték-feladatok differenciálszámítás nélkül, Gömb és részei, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1987/január: Gy.2389 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A két feladatra közös megoldást adunk. Azt állítjuk, hogy a körök maximális sugara mindkét esetben ugyanakkora, . Ehhez egyrészt megmutatjuk, hogy darab sugarú kör még elhelyezhető a gömbfelületen, viszont -nél nagyobb sugarú körökből már darab sem fér el a gömbön. 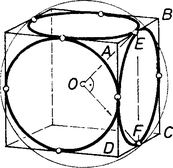 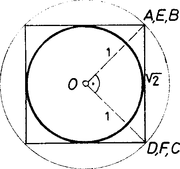 Tekintsünk egy olyan kockát, melynek minden éle érinti a gömböt (1. ábra). A kocka hat lapja hat kört metsz ki a gömbből, ezek éppen a kockalapok beírt körei. A kockaélek felezőpontjai illeszkednek a gömbfelületre, hiszen a szimmetria miatt a gömb éppen ezekben a pontokban érinti az éleket. Egy lap két szemközti élének felezőpontja, valamint a gömb középpontja egyenlő szárú, derékszögű háromszöget határoz meg, melynek befogói gömbsugarak, átfogója tehát . Az átfogó ugyanakkor a lemetszett körök átmérőjével egyenlő, így ezek sugara . Ez pedig azt jelenti, hogy darab sugarú kör elhelyezhető a feltételeknek megfelelően. Tegyük most fel, hogy elhelyeztünk darab egybevágó kört a gömbfelületen úgy, hogy azok nem metszik egymást. A körök sugara ekkor -nél kisebb, mert egy gömb bármely két főköre metszi egymást. Egyértelműen léteznek tehát a gömb középpontjából induló, az adott körök középpontján átmenő félegyeneseknek a gömbbel való metszéspontjai. Nevezzünk egy-egy ilyen pontot a szóban forgó kör ,,felületi középpontjának''. Nyilvánvaló, hogy annál nagyobb a körök sugara, minél nagyobb a felületi középpontok közül a két legközelebbinek a gömbi távolsága. (Két pont gömbi távolsága a két ponton átmenő főkörben a pontok közötti rövidebb ív hossza.) Mivel két érintkező, sugarú kör felületi középpontjának gömbi távolsága egységnyi sugarú gömbön éppen ‐ ez a helyzet az 1. ábrán bemutatott elrendezésben ‐ ezért az állítás második részéhez azt kell igazolnunk, hogy az öt felületi középpont közül nem lehet bármely kettő távolsága nagyobb -nél, más szóval, ha adott öt pont az egységnyi sugarú gömb felszínén, akkor a köztük fellépő gömbi távolságok minimuma nem nagyobb, mint . Legyen az öt pont , , , és , és rajzoljunk a gömbön három, páronként merőleges síkú főkört, ebből kettőt az -n keresztül úgy, hogy egyikük a ponton is áthaladjon. Ezek a főkörök a gömb felszínét egybevágó, egyenlő oldalú gömbháromszögre osztják, amelyek oldalának hossza éppen (2. ábra). 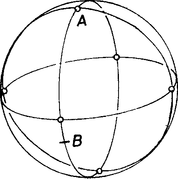 A megfelelő síkgeometriai tétel bizonyításához hasonlóan igazolható, hogy egy gömbháromszög bármely két pontjának a ‐ gömbi ‐ távolsága legfeljebb akkora, mint a gömbháromszög legnagyobb oldala. Így elegendő megmutatnunk, hogy a gömbfelszín iménti felosztását szolgáltató gömbháromszög között van olyan, amelyik legalább kettőt tartalmaz a megadott pont közül. Az pont négy gömbháromszögnek a csúcsa, és ha ezek egyikének sem pontja, ami föltehető, akkor e négytől különböző kettőnek a határán helyezkedik el. Amennyiben e hat gömbháromszög valamelyike tartalmazza a , a vagy az pontot, akkor az idézett segédtétel szerint készen vagyunk. Ha nem, akkor e pontot a megmaradó két gömbháromszög tartalmazza és így egyikük biztosan legalább -t tartalmaz. Ezzel állításunkat igazoltuk, az felületi középpont között valóban van olyan kettő, amelyek legfeljebb távolságra vannak egymástól a gömbön, vagyis a körök sugara nem lehet nél nagyobb. Megjegyzések. 1. Azt a meglepő tényt igazoltuk, hogy ha egy gömb felületén el tudunk helyezni egyenlő sugarú, nem metsző kört, akkor ezeket alkalmasan elmozgatva még egy hatodik ugyanilyen sugarú kör is elfér a gömbön. 2. A bizonyítás során egy síkgeometriai tétel gömbi változatát használtuk. A gömbfelületen nagyon sok síkgeometriai tétel megfelelője teljesül. Erről bővebben olvashattok pl. Szabó Endre: Sokszögek a gömbön (KÖMAL 1987/4. 147. old.) című cikkében. 3. A gyakorlat megoldóitól kevésbé precíz, a szemléletre jobban támaszkodó megoldásokat is elfogadtunk. |