Kezdőlap


Feladat:	Gy.2324	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Sustik Mátyás
Füzet:	1986/november, 393 - 394. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Alakzatok szimmetriái, Húrnégyszögek, Szabályos sokszögek geometriája, Gyakorlat
Hivatkozás(ok):	Feladatok: 1986/február: Gy.2324

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az $A_{6} A_{7}$ oldal felező merőlegese a hétszög (egyik) szimmetriatengelye. Az $A_{1} A_{3}$ és $A_{3} A_{5}$ , valamint $A_{2} A_{7}$ és $A_{4} A_{6}$ húrok egymás $f$ -re vonatkozó tükörképei, következésképp metszéspontjaik, $B_{1}$ és $B_{4}$ is tükrös helyzetűek. Hasonlóan $C_{1}$ és $C_{3}$ is szimmetrikus pontpár, ezért a feladat állítása következik abból, ha megmutatjuk: $C_{1}$ rajta van a $B_{1} B_{4}$ szakaszon, vagy ami ezzel ekvivalens, hogy 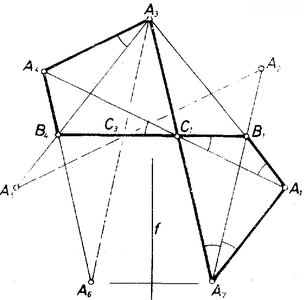$B_{4} C_{1} A_{4} ∢ = A_{1} C_{1} B_{1} ∢$ .

Most

C_{1} A_{7} B_{1} ∢ = A_{3} A_{7} A_{2} ∢ = A_{4} A_{1} A_{3} ∢ = C_{1} A_{1} B_{1} ∢

, hiszen a középső két szög a hétszög egy-egy oldalához tartozó kerületi szög. Ezért a

C_{1} B_{1} A_{1} A_{7}

négyszög húrnégyszög, és így

\begin{matrix} A_{1} C_{1} B_{1} ∢ = A_{1} A_{7} B_{1} ∢ = A_{1} A_{7} A_{2} ∢ . \end{matrix}

Hasonlóan

B_{4} A_{4} C_{1} ∢ = A_{6} A_{4} A_{1} ∢ = A_{5} A_{3} A_{7} ∢ = B_{4} A_{3} C_{1} ∢

, itt két-két szomszédos oldalhoz tartozó kerületi szög egyenlőségét használtuk ki. Így

B_{4} C_{1} A_{3} A_{4}

is húrnégyszög, tehát

\begin{matrix} B_{4} C_{1} A_{4} ∢ = B_{4} A_{3} A_{4} ∢ = A_{5} A_{3} A_{4} ∢ . \end{matrix}

Végül

A_{1} A_{7} A_{2} ∢

és

A_{5} A_{3} A_{4} ∢

egyenlősége következik például abból, hogy mindkettő a hétszög egy oldalához tartozó kerületi szöggel egyenlő.
Ezzel a feladat állítását beláttuk.

Megjegyzés. Sok megoldó trigonometriai azonosságok felhasználásával bizonyította az állítást. Ezek a megoldások az itt közöltnél hosszabbak és bonyolultabbak.