Kezdőlap


Feladat:	Gy.2308	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1986/szeptember, 262. oldal		PDF \| MathML
Témakör(ök):	Algebrai átalakítások, Ponthalmazok, Háromszögek nevezetes tételei, Magasságvonal, Súlypont, Terület, felszín, ( x + 1/x ) > = 2 ( x > 0 ), Párhuzamos szelők tétele, Gyakorlat
Hivatkozás(ok):	Feladatok: 1985/december: Gy.2308

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen $P$ a háromszög tetszőleges belső pontja! Jelöljük az $A P C$ háromszög területét $T_{B}$ -vel, a $B P C$ háromszög területét $T_{A}$ -val, az $A P B$ háromszög területét pedig $T_{C}$ -v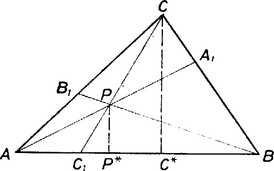el!

Bocsássunk merőlegeseket a

P

és a

C

pontokból az

A B

oldalra! Ezek talppontjai legyenek

P^{*}

és

C^{*}

.
Megmutatjuk, hogy

\begin{matrix} \frac{C C_{1}}{P C_{1}} = \frac{C C^{*}}{P P^{*}} . \end{matrix}

(1)

Ha a

P C

egyenes merőleges az

A B

egyenesre, akkor a

C_{1}

P^{*}

és

C^{*}

pontok egybeesnek, és (1) nyilvánvaló. Ha ezek a pontok nem esnek egybe, akkor a

P P^{*}

és

C C^{*}

egyenesek párhuzamossága miatt a párhuzamos szelők tételéből következik (1).
Tehát

\begin{matrix} \frac{C C_{1}}{P C_{1}} = \frac{C C^{*}}{P C^{*}} = \frac{C C^{*} \cdot \frac{A B}{2}}{P P^{*} \cdot \frac{A B}{2}} = \frac{T_{A} + T_{B} + T_{C}}{T_{C}} . \end{matrix}

Ugyanígy kapjuk, hogy

\begin{matrix} \frac{A A_{1}}{P A_{1}} = \frac{T_{A} + T_{B} + T_{C}}{T_{A}} és \frac{B B_{1}}{P B_{1}} = \frac{T_{A} + T_{B} + T_{C}}{T_{B}} . \end{matrix}

Vagyis a háromszög tetszőleges

P

belső pontjára

\begin{matrix} \frac{A A_{1}}{P A_{1}} + \frac{B B_{1}}{P B_{1}} + \frac{C C_{1}}{P C_{1}} = \frac{T_{A} + T_{B} + T_{C}}{T_{A}} + \frac{T_{A} + T_{B} + T_{C}}{T_{B}} + \frac{T_{A} + T_{B} + T_{C}}{T_{C}} = \\ = 3 + (\frac{T_{B}}{T_{A}} + \frac{T_{A}}{T_{B}}) + (\frac{T_{C}}{T_{A}} + \frac{T_{A}}{T_{C}}) + (\frac{T_{C}}{T_{B}} + \frac{T_{B}}{T_{C}}) \geq 3 + 3 \cdot 2 = 9, \end{matrix}

mert egy pozitív számnak és a reciprokának az összege legalább

2

.
Tehát a háromszög tetszőleges belső pontjára igaz az állítás.
Egyenlőség akkor áll fenn, ha

T_{A} = T_{B} = T_{C}

, vagyis ha

P

a háromszög súlypontja.