Kezdőlap


Feladat:	Gy.2179	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Ájus F. , Balázs Á. , Bodrogi 365 Zs. , Csalánosi T. , Csott R. , Dinnyés Enikő , Ezer Éva , Gyuris T. , Gyüre P. , Hámori 967 Tünde , Heller Judit , Horváth S. , Horváth Sándor , Karsai T. , Kerey P. , Király Andrea , Klug R. , Kocsis Z. , Kucsera Itala , Ládonyi F. , Licsik I. , Ligeti Z. , Molnár K. , Montágh B. , Nagy J. , Nausch Á. , Némedi Varga Zs. , Nusser Z. , Papp 694 L. , Regős G. , Szabó 212 Z. , Szabó 529 G. , Szabó 544 A. , Szigeti Z. , Szinku Zs. , Szoboszlai L. , Tóth 324 T. , Török B. , Zsigmond L.
Füzet:	1985/január, 18 - 20. oldal		PDF \| MathML
Témakör(ök):	Középpontos és egyéb hasonlósági transzformációk, Súlypont, Terület, felszín, Egyéb sokszögek geometriája, Gyakorlat
Hivatkozás(ok):	Feladatok: 1984/február: Gy.2179

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a nagyítás után kapott háromszög csúcsait rendre $K$ , $L$ , $M$ -mel, ahol $K$ a $P$ -vel szemközti csúcs. Tudjuk, hogy az $A B C$ háromszög az $R Q P$ háromszög $S$ súlypontjából $- \frac{1}{2}$ arányú kicsinyítéssel jött létre, azaz e két háromszög súlypontja megegyezik. Jelölje a $P B$ súlyvonal és $A C$ oldal metszéspontját $P_{1}$ , ekkor $P P_{1} = \frac{1}{2} P B$ , $P S = \frac{2}{3} P B$ , ahonnan $P S = 4 P_{1} S$ . Az $L M$ szakasz metszi a $P P_{1}$ szakaszt, és így a $P Q R$ háromszög $P A$ , $P C$ oldalszakaszait is. Ez pedig azt jelenti, hogy a $D_{1} D_{2} E_{1} E_{2} F_{1} F_{2}$ valódi (konvex) hatszög. Ha viszont $k \leq 1$ , akkor a $K L M$ képháromszög kisebb, mint az eredeti $A B C$ háromszög; ha pedig $k \geq 4$ , akkor a képháromszög tartalmazza a $P Q R$ háromszöget, a megfelelő oldalak nem metszik egymást, nem jön létre hatszög.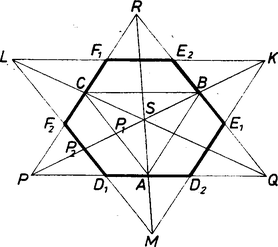

1. ábra

Legyen tehát

1 < k < 4

, és jelöljük a

P P_{1}

és

D_{1} F_{2}

szakaszok metszéspontját

P_{2}

-vel. Az

A B C

és

M K L

háromszögek hasonlósága miatt

\begin{matrix} \frac{P_{2} S}{P_{1} S} = k, \end{matrix}

és így

\begin{matrix} \frac{P P_{2}}{P_{1} S} = \frac{P S - P_{2} S}{P_{1} S} = \frac{P S}{P_{1} S} - \frac{P_{2} S}{P_{1} S} = 4 - k . \end{matrix}

P D_{1} F_{2}

F_{1} E_{2} R

D_{2} Q E_{1}

háromszögek mindegyike hasonló a

P Q R

háromszöghöz, és a hasonlóság aránya

P B = 3 \cdot B S = 3 \cdot (2 \cdot P_{1} S)

alapján

\begin{matrix} λ = \frac{P P_{2}}{P B} = \frac{P P_{2}}{6 P_{1} S} = \frac{4 - k}{6}, \end{matrix}

(1)

mindhárom esetben. A kis háromszögek tehát egybevágóak, területük a

P Q R

háromszög területének

λ^{2}

-szerese.
Jelöljük a

P Q R

háromszög területét

T

-vel. A hatszög területét úgy kaphatjuk meg, hogy

T

-ből kivonjuk a

3

kis háromszög területének összegét. Ennek kell kétszer akkorának lennie, mint az

A B C

háromszög területe. Ám az

A B C

háromszög területe

T / 4

, ezért a következő összefüggésnek kell fennállnia:

T - 3 λ^{2} T = T / 2

, azaz

λ^{2} = 1 / 6

. A

λ

helyébe az (1) szerinti

(4 - k) / 6

-ot helyettesítve

{(4 - k)}^{2} = 6

, amit az

1 < k < 4

feltétel mellett csak a

k = 4 - \sqrt[]{6}

érték elégít ki.
Így

k

értéke csak

4 - \sqrt[]{6}

lehet. Ha

k

-t ennyinek választjuk, (1) alapján az egybevágó

P D_{1} F_{2}

F_{1} E_{2} R

D_{2} Q E_{1}

háromszögek a

P Q R

háromszögből

λ = = \sqrt[]{6} / 6

arányú kicsinyítéssel jönnek létre, tehát a hatszög területe

\begin{matrix} T - 3 λ^{2} T = T - \frac{1}{2} T = \frac{1}{2} T, \end{matrix}

valóban megegyezik az

A B C

háromszög területének kétszeresével.

Megjegyzések. 1. A feltételként kapott

{(4 - k)}^{2} = 6

egyenletet a

k = 4 - \sqrt[]{6}

értéken kívül a

k = 4 + \sqrt[]{6}

is kielégíti. Mi lehet ennek a második megoldásnak a geometriai jelentése? Az

A B C

háromszöget

(4 + \sqrt[]{6})

-szorosára kinagyítva, a kapott

M K L

háromszög oldalai nem metszik a

P Q R

háromszög oldalszakaszait, hanem csak oldalegyeneseit. A keletkezett

D_{1} D_{2} E_{1} E_{2} F_{1} F_{2}

idom "hurkolt'' hatszög. Ha ennek "területét'' úgy definiáljuk, hogy a

P Q R

háromszög területéből levonjuk a vonalkázott "hurkok'' területét, akkor erre a hatszögre is teljesül, hogy "területe'' kétszerese az

A B C

háromszög területének (2. ábra).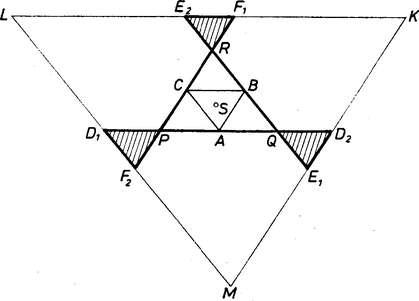

2. ábra

2. A maximális pontszámot azok kapták meg, akik azt is indokolták, hogy a

{(4 - k)}^{2} = 6

egyenlet megoldásaként adódó

k = 4 - \sqrt[]{6}

miért megoldása a feladatnak is (és nemcsak ennek az egyenletnek), illetve hogy a másik,

k = 4 + \sqrt[]{6}

miért nem megoldás.