Kezdőlap


Feladat:	Gy.2098	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Balog 444 P. , Barsi S. , Bíborka Judit , Boros 966 Z. , Bujdosó 419 L. , Czabarka Éva , Edvi T. , Füst Á. , Giba P. , Grallert Ágnes , Gróf A. , Hraskó A. , Jedlovszky P. , Kónya Eszter , Kós G. , Magyar P. , Megyesi Gábor , Papp 710 Zs. , Porkoláb L. , Simon Gy. , Somogyi 196 A. , Zsigri G.
Füzet:	1983/november, 138. oldal		PDF \| MathML
Témakör(ök):	Súlyvonal, Terület, felszín, Egyéb sokszögek geometriája, Gyakorlat, Középvonal, Háromszögek hasonlósága
Hivatkozás(ok):	Feladatok: 1983/január: Gy.2098

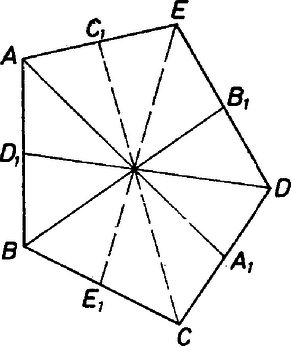
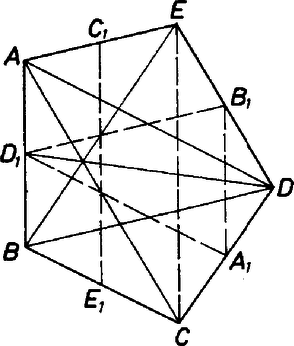
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelölje $A$ , $B$ , $C$ , $D$ , $E$ az ötszög csúcsait és legyen az $A$ csúccsal szemközti oldal felezőpontja $A_{1}$ , a $B$ -vel szemközti oldal felezőpontja $B_{1}$ . és így tovább. Először megmutatjuk, hogy $A B ∥ A_{1} B_{1} ∥ C E ∥ C_{1} E_{1}$ .

Jelöljük az

X

Y

Z

pontok által meghatározott háromszög területét

t_{X Y Z}

-vel.
Feltétel szerint

\begin{matrix} t_{A D_{1} D} + t_{A D E} = t_{B D_{1} D} + t_{B D C} . \end{matrix}

D D_{1}

súlyvonal felezi az

A B D

háromszög területét:

t_{A D_{1} D} = t_{B D_{1} D}

, és ezért

t_{A D E} = t_{B D C}

. Hasonlóan kapjuk, hogy

t_{A B E} = t_{E D C} = t_{E A B} = t_{B C D} = t_{A D E}

.
Az

A B C

és

A B E

közös alapú, egyenlő területű háromszögek, ezért

E

és

C

egyenlő távol van az

A B

egyenestől, azaz

A B ∥ C E

. Az

A B C E

trapézban

C_{1} E_{1}

középvonal, a

C E D

háromszögben pedig az

A_{1} B_{1}

középvonal, ezért

E_{1} C_{1} ∥ E C ∥ A B ∥ A_{1} B_{1}

. Ezzel igazoltuk állításunkat.
Ugyanígy kapjuk, hogy

A D ∥ A_{1} D_{1}

és

B D ∥ B_{1} D_{1}

, vagyis az

A B D

és

A_{1} B_{1} D_{1}

háromszögek oldalai páronként párhuzamosak. A két háromszög tehát centrálisan hasonló. A megfelelő csúcsaikat összekötő szakaszok átmennek a centrumon,

A A_{1}

B B_{1}

és

D D_{1}

tehát egy pontban metszik egymást.
Abból, hogy az

A C D

és

A_{1} C_{1} D_{1}

háromszögek megfelelő oldalai párhuzamosak, kapjuk, hogy

A A_{1}

és

D D_{1}

metszéspontján átmegy

C C_{1}

is. Végül a

B D E

és a

B_{1} D_{1} E_{1}

háromszögek centrális hasonlóságából adódik, hogy ezt a közös pontot

E E_{1}

is tartalmazza.

Megyesi Gábor (Szeged, Ságvári E. Gyak. Gimn., II. o. t.)
dolgozata alapján

Megjegyzések. 1. Sok megoldó próbálta " fizikusan'' megoldani a feladatot. Ezek még fizikai szempontból is hibásak, így természetesen nem kaptak pontot. Mások tudni, ill. bizonyítani vélték, hogy a feltételeknek megfelelő ötszög mindig szabályos. Ez nem igaz.
2. Legyen adva a síkon egy

e

egyenes és egy

λ > 0

valós szám. Az

e

egyenesre vonatkozó

λ

arányú merőleges affinitásnak nevezzük a következő transzformációt: Tekintsük az

e

egyenest egy derékszögű koordináta‐rendszer

x

-tengelyének, és az

(x, y)

pontot vigye a transzformáció a

(λ x, y)

pontba. Az affinitással való ismerkedésképpen érdemes bebizonyítani az alábbi tulajdonságokat: az affinitás egyenest egyenesbe visz; egy egyenesen levő pontok távolságarányát megtartja; síkidomok területének arányát megtartja. Ezek alapján belátható, hogy a szabályos ötszög affin képei eleget tesznek a feladat feltételeinek. A feladatban szereplő tulajdonsággal bíró ötszögek pontosan azok, amelyek a szabályos ötszögből legfeljebb két affinitással keletkeznek. Ennek bizonyítását nem részletezzük.