Kezdőlap


Feladat:	Gy.1949	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Alberi G. , Almási Cs. , Balázs Z. , Bodár Á. , Böröczky K. , Böröczky L. , Csúri Piroska , Ditrich P. , Dudás Katalin , Erdős L. , Fabinyi G. , Fekete Zs. , Fonyó L. , Hauk Gabriella , Hetyei Judit , Hitre Erika , Ittzés A. , Károlyi Gy. , Kiss I. , Kiss P. , Kocsis Csilla , Makra Zsuzsa , Mohay T. , Nagy R. , Németh Á. , Papp G. , Párkányi I. , Seregdy T. , Szabó E. , Tóth G. , Vadvári T. , Weisz F. , Zieger B. , Zoltai L.
Füzet:	1981/május, 207 - 208. oldal		PDF \| MathML
Témakör(ök):	Mértani helyek, Húrnégyszögek, Gyakorlat
Hivatkozás(ok):	Feladatok: 1980/december: Gy.1949

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ha $γ = A C B ∢ = 90^{\circ}$ , akkor az $A P$ , ill. $P B$ szakasz a $k_{1}$ , $k_{2}$ körnek átmérője $P A' | | B C$ , $P B' | | A C$ miatt. A két körnek tehát nincsen második metszéspontja (1. ábra).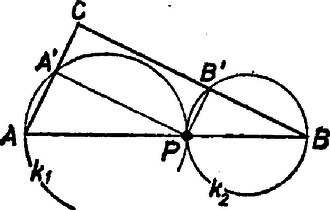

1. ábra

A továbbiakban elég azt a két esetet vizsgálni, amikor

γ < 90^{\circ}

, ill.

γ > 90^{\circ}

.
Ha

γ < 90^{\circ}

, akkor nyilván az

A A' P ∢

és a

B B' P ∢

is kisebb

90^{\circ}

-nál, s ezért a

k_{1}

k_{2}

körök

O_{1}

, ill.

O_{2}

középpontja az

A B

egyenesnek a

C

-t tartalmazó partjára esik (2. ábra).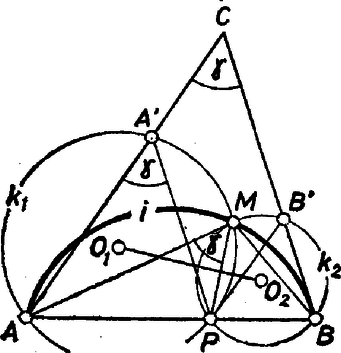

2. ábra

M

is ugyanazon partján van az

A B

-nek, mint

C

, hiszen

O_{1} O_{2}

merőlegesen felezi a

P M

szakaszt. Így

\begin{matrix} A M P ∢ = A A' P ∢ és P M B ∢ = P B' B ∢ \end{matrix}

egy íven nyugvó kerületi szögek. Az egyenlőség jobb oldalán álló szögek egyállásúak

γ

-val, és így egyenlők. Ebből

A M B ∢ = 2 γ

M

tehát azon a köríven van, melynek pontjaiból az

A B

szakasz

2 γ

szög alatt látszik és

A B

-nek ugyanazon partján fekszik, mint

C

.
Ha

γ

tompaszög, akkor

M

A B

-nek ellenkező partján van, mint

C

(3. ábr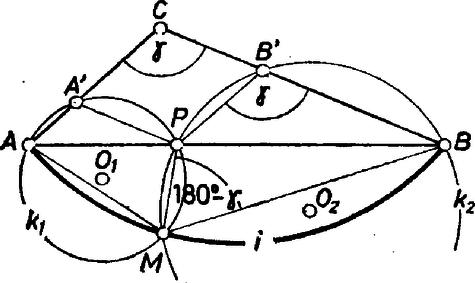a).

3. ábra

Most mivel az

A A' P M

, ill.

B B' P M

húrnégyszögben

A M P ∢ = B M P ∢ = 180^{\circ} - γ

M

azon a köríven van, melyből az

A B

oldal

360^{\circ} - 2 γ

szögben látszik. Természetesen az

A

B

végpontok egyik esetben sem tartoznak a mértani helyhez.
Mindkét esetben az

i

körív minden belső pontja a mértani helyhez tartozik. Legyen ugyanis

M

egy tetszőleges pontja

i

-nek. Messe az

A M B ∢

szögfelezője az

A B

-t

P

-ben.

P

-ből kiindulva szerkesszük meg

A', B'

-t. Ekkor vagy

A M P ∢ = A A' P ∢

és

B M P ∢ = B B' P ∢

; vagy

A A' P ∢ + A M P ∢ = B B' P ∢ + B M P ∢ = 180^{\circ}

és ezért

M

A,

A'

P

, ill.

M

B

B'

P

mindig egy-egy körön vannak, s a két körnek valóban

M

a közös pontja.

Csúri Piroska (Szeged, JATE Ságvári E. Gyak. Gimn., II. o. t.)