| Feladat: | Gy.1843 | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Füzet: | 1980/február, 67 - 68. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Alakzatba írt kör, Beírt alakzatok, Tengelyes tükrözés, Derékszögű háromszögek geometriája, Terület, felszín, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1979/május: Gy.1843 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Jelöljük az átmérő végpontjait , -val, a négyzet csúcsait , , , -vel, és legyen a -n levő, azzal megegyező irányítású oldal. Tükrözzük a négyzetet -ra, kapjuk , tükörképeként a , csúcsokat. A háromszög területe fele a téglalap területének, ami viszont területének kétszerese. Így a háromszög átfogóját a kör középpontja körül -ba forgatva, épp a feladatban szereplő háromszög csúcsába kerül, és ebben kétszerese -nek csakúgy, mint a -nek. 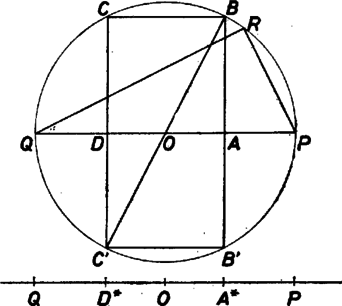 Jelöljük a háromszög kerületének felét -sel, a beírt kör -n levő pontját -gal. Azt kell megmutatnunk, hogy azonos -val. Jelöljük még -ra vonatkozó tükörképét -gal. Nyilván elegendő megmutatnunk, hogy . Ismeretes, hogy , , emiatt , hiszen fele -nak. Azt viszont már beláttuk, hogy egyenlő a négyzet oldalával, a bizonyítást ezzel befejeztük. Megjegyzés. A megoldás élt a feladat hallgatólagos feltevésével, hogy a szóban forgó háromszög egyértelműen meghatározott, pontosabban mondva csak az általunk megkonstruált háromszög és annak felezőmerőlegesére vonatkozó tükörképe egyenlő területű a négyzettel. Ez azért van így, mert a háromszög területe és átfogója már meghatározza az átfogóhoz tartozó magasságot. |