Kezdőlap


Feladat:	Gy.1821	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1979/november, 147 - 148. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Derékszögű háromszögek geometriája, Magasságvonal, Gyakorlat
Hivatkozás(ok):	Feladatok: 1979/február: Gy.1821

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A bizonyításhoz felhasználjuk, hogy ha egy külső $P$ pontból egy körhöz érintőt és szelőt húzunk, akkor az érintőszakasz hossza mértani középarányosa a szelődaraboknak, $P E^{2} = P X \cdot P Y$ . (Lásd a II. o. tankönyv 175. oldal 240. feladat.)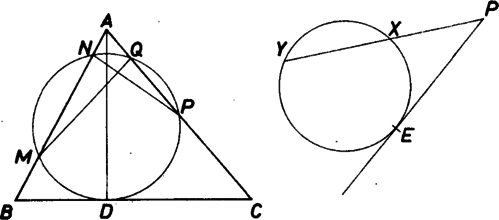

Ezt alkalmazva először a

B

pontból kiinduló érintőre és szelőre

B D^{2} = B M \cdot B N

. Mivel

M

N

A B

oldalra esik, kifejezhetjük két szakasz különbségeként

\begin{matrix} B D^{2} = (A B - A M) (A B - A N) = A B^{2} - A B (A N + A M) + A M \cdot A N . \end{matrix}

Átrendezve és felhasználva az

A D C

háromszögben Pitagorász tételét:

\begin{matrix} A B (A M + A N) = A B^{2} - B D^{2} + A M \cdot A N = A D^{2} + A M \cdot A N . \end{matrix}

(2)

Az egyenlőség bal oldalán álló kifejezés megegyezik (1) bal oldalával, közös nevezőre hozás után.
Hasonlóan kapjuk, hogy

\begin{matrix} C D^{2} = C P \cdot C Q = (A C - A P) (A C - A Q) = A C^{2} - A C (A P + A Q) + A P \cdot A Q . \\ A C (A P + A Q) = A C^{2} - C D^{2} - A P \cdot A Q = A D^{2} + A P \cdot A Q . & (3) \end{matrix}

Ennek bal oldala pedig (1) jobb oldalával egyenlő.
Már csak a (2) és (3) jobb oldalán álló kifejezések egyenlőségét kell belátnunk. Ehhez vegyük észre, hogy az

A P N

és

A Q M

háromszögek hasonlók. Az

A

csúcsnál levő szögük közös,

A P N ∢ = A M Q ∢

ugyanazon íven nyugvó kerületi szögek. A hasonlóság miatt

A M : A P = A Q : A N

, ahonnan

A P \cdot A Q = A N \cdot A M

. Tehát az (1) egyenlőség valóban fennáll.