Kezdőlap


Feladat:	Gy.1682	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Albu Ildikó , Boros T. , Fazekas G. , Hajnal P. , Kálmán J. , Kántor S. , Kátai I. , Kőrösi G. , Lakatos I. , Mádl F. , Németh R. , Oláh K. , Petre P. , Pintér 395 F. , Schwarcz P. , Szegedi M. , Szendrei Gy. , Varga T. , Veszprémi P. , Winkler R.
Füzet:	1977/november, 140 - 141. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Körülírt kör, Magasságpont, Hossz, kerület, Szögfüggvények, síkgeometriai számítások, Gyakorlat
Hivatkozás(ok):	Feladatok: 1977/február: Gy.1682

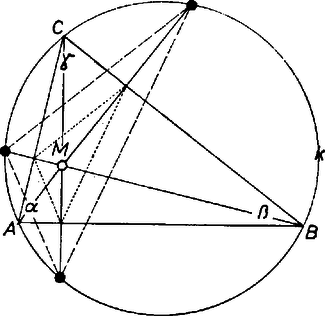
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a háromszög csúcsait $A$ , $B$ , $C$ -vel, szögeit $α$ , $β$ , $γ$ -val, magasságpontját $M$ -mel, körülírt körét $k$ -val, és válasszuk egységnek $k$ sugarát.

Ekkor a háromszög félkerülete, mint ismeretes

\begin{matrix} s = sin α + sin β + sin γ . \end{matrix}

Az is ismert, hogy

M

-nek az oldalakra vonatkozó tükörképei

k

-n vannak, tehát ennek a háromszögnek is a szögei szinuszának az összege a fél kerülete:

\begin{matrix} s_{M} = sin α_{M} + sin β_{M} + sin γ_{M}, \end{matrix}

ahol az

M

index a magasságpontra utal. Ha a háromszög hegyesszögű, akkor

\begin{matrix} α_{M} = 180^{\circ} - 2 α, β_{M} = 180^{\circ} - 2 β, γ_{M} = 180^{\circ} - 2 γ, \end{matrix}

ha pedig mondjuk

C

-nél tompaszög van, akkor

\begin{matrix} α_{M} = 2 α, β_{M} = 2 β, γ_{M} = 2 γ - 180^{\circ} . \end{matrix}

Így tehát mindkét esetben

\begin{matrix} s_{M} = | sin 2 α | + | sin 2 β | + | sin 2 γ |, \end{matrix}

ami akkor is helyes, ha a háromszög derékszögű. Azt kell megvizsgálnunk, hogy következik-e az

s_{M} = s

feltétellel ekvivalens

\begin{matrix} sin α + sin β + sin γ = | sin 2 α | + | sin 2 β | + | sin 2 γ | \end{matrix}

(1)

feltételből az, hogy

α = β = γ = 60^{\circ}

?
Ha a háromszög hegyesszögű, akkor igen, hiszen

\begin{matrix} sin 2 α + sin 2 β ≧ 2 sin (α + β), \\ sin 2 β + sin 2 γ ≧ 2 sin (β + γ), & (2) \\ sin 2 γ + sin 2 α ≧ 2 sin (γ + α) \end{matrix}

miatt mindig igaz, hogy ha

α + β + γ = 180^{\circ}

, akkor

\begin{matrix} sin 2 α + sin 2 β + sin 2 γ ≧ sin α + sin β + sin γ, \end{matrix}

és az egyenlőség pozitív

α

β

γ

-ra csak

α = β = γ

mellett állhat fenn.

Ha viszont találunk (1)-nek olyan megoldását, melyben mondjuk

γ > 90^{\circ}

, akkor a feladat állítása nyilván nem igaz. Olyan

α

β

szögeket keresünk tehát, amelyek pozitívak, összegük kisebb, mint

90^{\circ}

, és teljesül rájuk, hogy

\begin{matrix} sin α + sin β + sin (α + β) = sin 2 α + sin 2 β + sin (2 α + 2 β) . \end{matrix}

(3)

Használjuk fel a

\begin{matrix} sin 2 α + sin 2 β = 2 sin (α + β) cos (α - β) \end{matrix}

(4)

összefüggést [amiből (2) is következik]:

\begin{matrix} 2 sin \frac{α + β}{2} cos \frac{α - β}{2} + sin (α + β) = & (5) \\ = 2 sin (α + β) cos (α - β) + sin (2 α + 2 β) . \end{matrix}

Rögzített

(α + β)

mellett ez a

cos \frac{α - β}{2}

ismeretlenre másodfokú egyenlet. Ha találunk olyan

(α + β)

értéket, amely mellett (5)-nek

cos \frac{α - β}{2}

-re van

1

és

cos \frac{α + β}{2}

közti gyöke, megvan az ellenpélda. Nézzük meg a két oldal különbségét ezeken a helyeken. Ha

cos \frac{α - β}{2}

helyére

1

-et írunk, a jobb és bal oldal különbsége

\begin{matrix} sin (2 α + 2 β) + sin (α + β) - 2 sin \frac{α + β}{2}, \end{matrix}

ha pedig

cos \frac{α + β}{2}

-t írunk a helyére, a különbség

\begin{matrix} 2 (sin (2 α + 2 β) - sin (α + β)) . \end{matrix}

α + β = 60^{\circ}

, ez utóbbi éppen

0

, ha pedig

α + β > 60^{\circ}

, akkor negatív. Az első különbség

α + β = 60^{\circ}

mellett pozitív, ha tehát

α + β

kicsit túllépi a

60^{\circ}

-ot, a két különbség ellenkező előjelű: az első pozitív, a második negatív. (Könnyen látható, hogy például

α + β = 70^{\circ}

megfelel.)
A feladat állítása tehát nem igaz.

Megjegyzés. Ha (5)-be az

α - β = 0

értéket helyettesítjük,

cos \frac{α + β}{2}

-re harmadfokú egyenletet kapunk. A megoldók többsége erről látta be, hogy van gyöke. Ehhez az ún. Bolzano-tételt kellett használniuk, mely szerint, ha egy zárt intervallumban folytonos függvény az intervallum elején pozitív, a végén negatív, akkor valahol az intervallum belsejében

0

-val egyenlő. Nekünk ezt csak másodfokú függvényre kellett felhasználnunk, ami a függvény ismert menetéből (és a másodfokú egyenlet megoldóképletéből) következik.