Kezdőlap


Feladat:	Gy.1681	Korcsoport: 14-15	Nehézségi fok: -
Megoldó(k):	Csikós B. , Csordás A. , Filakovszky P. , Gát Gy. , Hajnal P. , Kiss 171 Zs. , Korondi P. , Lukács Erzsébet , Marosi 961 I. , Molnár 267 T. , Molnár 338 A. , Pacher T. , Szeles J. , Varga Lívia , Varga T. , Veszprémi P.
Füzet:	1978/május, 204 - 205. oldal		PDF \| MathML
Témakör(ök):	Középpontos és egyéb hasonlósági transzformációk, Súlypont, Háromszögek szerkesztése, Vektorok lineáris kombinációi, Helyvektorok, Gyakorlat
Hivatkozás(ok):	Feladatok: 1977/február: Gy.1681

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladatot mindjárt az általános alakjában oldjuk meg. Legyen tehát $C_{1}$ , $A_{1}$ , $B_{1}$ az $A B$ , $B C$ , $C A$ szakaszoknak az a pontja, melyre

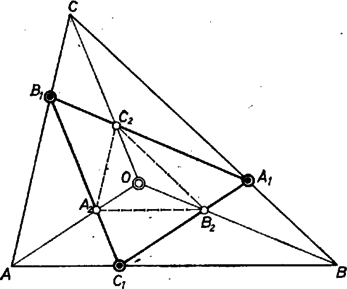\begin{matrix} A C_{1} : C_{1} B = B A_{1} : A_{1} C = C B_{1} : B_{1} A = p : q . \end{matrix}

(1)

Jelöljük a

p / (p + q)

q / (p + q)

hányadosokat

λ

-val,

μ

-vel. Mivel

p

q

egy-egy szakasz hossza,

λ

μ

pozitívak, és összegük

1

. Legyen

O

tetszőleges pont, és jelöljük általában az

O

-ból valamely nagy betűvel jelölt pontba mutató vektort megfelelő kis betűvel. Mivel az

X Y

szakaszt

p : q

arányban osztó

Z

pontra

\begin{matrix} z = x + λ \vec{X Y} = x + λ (y - x) = μ x + λ y, \end{matrix}

(1) ekvivalens a

\begin{matrix} c_{1} = μ a + λ b; a_{1} = μ b + λ c; b_{1} = μ c + λ a \end{matrix}

(2)

egyenletekkel.
Szorozzuk meg (2)-ben az első egyenletet

λ

-val, a másodikat

μ

-vel:

\begin{matrix} λ c_{1} + μ a_{1} = λ μ a + (λ^{2} + μ^{2}) b + λ μ c = λ μ (a + b + c) + (1 - 3 λ μ) b, \end{matrix}

(3)

hiszen

1 - 3 λ μ = {(λ + μ)}^{2} - 3 λ μ = λ^{2} - λ μ + μ^{2}

. Az itt fellépő

(a + b + c)

összeg (2) szerint egyenlő

(a_{1} + b_{1} + c_{1})

-gyel, és mindkettő

0

-val egyenlő, ha

O

-nak

A_{1} B_{1} C_{1}

súlypontját választjuk.
Azt kaptuk tehát, hogy

b = κ c_{2}

, ahol

c_{2} = λ c_{1} + μ a_{1}

, és

κ = 1 / (1 - 3 λ μ)

. Hasonlóan kapjuk

a

c

értékeit is, tehát

\begin{matrix} a = κ a_{2}, b = κ b_{2}, c = κ c_{2}, \end{matrix}

(4)

ahol

a_{2}

b_{2}

c_{2}

O

-ból az

A_{2}

B_{2}

C_{2}

pontokba mutató vektorok, és

A_{2}

B_{2}

C_{2}

rendre a

B_{1} C_{1}

C_{1} A_{1}

A_{1} B_{1}

szakaszoknak azon pontjai, amelyekre

\begin{matrix} B_{1} A_{2} : A_{2} C_{1} = C_{1} B_{2} : B_{2} A_{1} = A_{1} C_{2} : C_{2} B_{1} = q : p . \end{matrix}

(5)

A_{1}

B_{1}

C_{1}

pontok alapján az

A_{2}

B_{2}

C_{2}

pontok megszerkeszthetők, és ezekből (4) alapján a keresett

A

B

C

pontokat az

A_{1} B_{1} C_{1}

háromszög súlypontjából való

κ = 1 / (1 - 3 λ μ) = {(p + q)}^{2} / (p^{2} - p q + q^{2})

arányú nagyítással kapjuk meg.
Mivel

p^{2} + q^{2} > p q

κ

mindig nagyobb

1

-nél, ha

p = 1

q = 2

, akkor

κ = 3

. Behelyettesítéssel meggyőződhetünk róla, hogy a (4) alatti értékek kielégítik a (2) egyenleteket, ha

\begin{matrix} a_{2} = λ b_{1} + μ c_{1}, b_{2} = λ c_{1} + μ a_{2}, c_{2} = λ a_{1} + μ b_{1} . \end{matrix}

(6)

Például (3)-hoz hasonlóan

\begin{matrix} μ c_{2} + λ a_{2} = λ μ a_{1} + (λ^{2} + μ^{2}) b_{1} + λ μ c_{1} = λ μ (a_{1} + b_{1} + c_{1}) + (1 - 3 λ μ) b_{1}, \end{matrix}

és itt

O

választása miatt

a_{1} + b_{1} + c_{1} = 0

. Így

μ c + λ a = κ (μ b_{2} + λ a_{2}) = κ (1 - 3 λ μ) b_{1} = b_{1}

, amint azt bizonyítani akartuk.
Mivel az

A

B

C

pontok nincsenek egy egyenesen, az

A_{1}

B_{1}

C_{1}

pontok sem lehetnek egy egyenesen. Különben tetszőleges, nem egy egyenesen levő

A_{1}

B_{1}

C_{1}

ponthármashoz mindig pontosan egy megoldást kapunk.

Megjegyzés. Centrális nagyítás helyett egyszerűbben fejezhető be a szerkesztés úgy, hogy az

A_{1}

B_{1}

C_{1}

pontokon át rendre párhuzamosakat húzunk a

B_{2} C_{2}

C_{2} A_{2}

A_{2} B_{2}

egyenesekkel. Ennek az eljárásnak a helyességét azonban nehezebb belátni. Sokféleképpen megoldható a feladatunk, ha már tudjuk, hogy van megfelelő

A B C

háromszög. A megoldók többsége azonban adós maradt annak megmutatásával, hogy van ilyen háromszög, ami esetenként annak bizonyítását jelenti, hogy amit megszerkesztettek, az a keresett háromszög.