Kezdőlap


Feladat:	1609. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: -
Füzet:	1976/április, 168. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Alakzatok hasonlósága, Alakzatba írt kör, Körök, Gyakorlat
Hivatkozás(ok):	Feladatok: 1975/december: 1609. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a körszeletet határoló kört és egyenest $k$ -val, illetve $e$ -vel, a két érintő kört $k_{1}$ -gyel, $k_{2}$ -vel, a körök középpontját $O$ -val, $O_{1}$ -gyel és 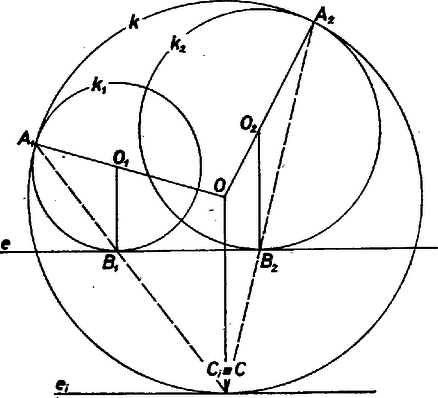$O_{2}$ -vel.

A következő megállapítások az

i = 1

és

i = 2

értékekre egyaránt érvényesek lesznek. Mivel

k_{i}

belülről érinti

k

-t

A_{i}

-ben,

O

A_{i} O_{i}

, félegyenesen van. Mivel

k_{i}

érinti

e

-t

B_{i}

-ben,

O_{i} B_{i}

, merőleges

e

-re.
Tekintsük azt az

A_{i}

centrumú nagyítást, mely

O_{i}

-t

O

-ba viszi. Jelöljük

B_{i}

pont megfelelőjét

C_{i}

-vel, az

e

egyenesét pedig

e_{i}

-vel. Mivel ez a nagyítás

k_{i}

-t

k

-ba viszi,

C_{i}

k

kör pontja, és

e_{i}

k

e

-vel párhuzamos érintője. A

k

körnek csak két,

e

-vel párhuzamos érintője van, ezek közül

e_{i}

csak az lehet, amelyik

e

-nek a körszelettel ellentétes oldalán van, hiszen a nagyítás miatt

e

elválasztja

A_{i}

-t

e_{i}

-től. Tehát az

e_{i}

egyenes helyzete nem függ

k_{i}

megválasztásától, így nem függ attól a

C_{i}

pont helyzete sem:

C_{i}

azonos azzal a

C

ponttal, amelyben

k

-nak az

e

-re merőleges ármérője metszi

k

-nak a körszelethez nem tartozó ívét. Mivel

A_{1} B_{1}

is,

A_{2} B_{2}

is átmegy ezen a

C

ponton,

C

egyben e két egyenes metszéspontja, (ha

k_{1}

nem azonos

k_{2}

-vel, a két egyenesnek más közös pontja nem lehet), ezzel a feladat állítását bebizonyítottuk.

Megjegyzés. Ha nagyítás helyett az

A_{i} B_{i} O_{i}

A_{i} C_{i} O

háromszögek hasonlóságát használjuk, külön kell foglalkozni azzal az esettel, amikor

A_{i} B_{i}

átmérő

k_{i}

-ben.