Kezdőlap


Feladat:	1604. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: -
Megoldó(k):	Józsa Miklós
Füzet:	1976/április, 165 - 166. oldal		PDF \| MathML
Témakör(ök):	Alakzatok köré írt kör, Gyakorlat
Hivatkozás(ok):	Feladatok: 1975/november: 1604. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feltétel szerint 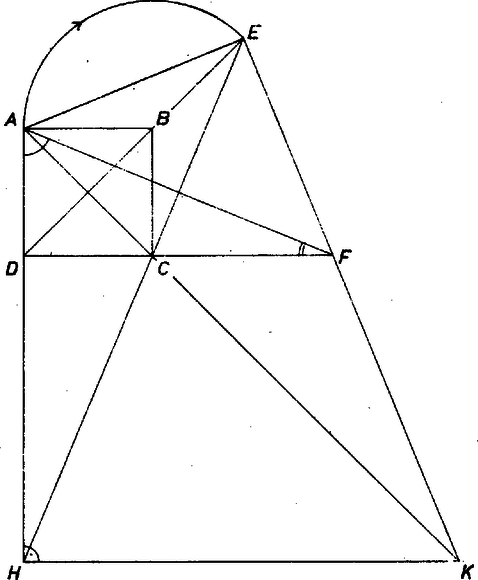$F A D ∢ = 3 \cdot A F D ∢$ és $F A D ∢ + A F D ∢ = 90^{\circ}$ , ezért $A F D ∢ = {22, 5}^{\circ} .$

A B E

háromszög egyenlő szárú

(A B = B E)

B

csúcsnál levő külső szöge

45^{\circ}

-os, így a háromszög

A E

alapján fekvő belső szögek

{22, 5}^{\circ}

-osak. Ez egyúttal azt is jelenti, hogy

A E D ∢ = {22, 5}^{\circ}

.
Az

A E F D

(konvex) négyszög oldala tehát az

E

és az

F

csúcsból egyaránt

{22, 5}^{\circ}

-os szög alatt látszik, s mivel az

E

és

F

csúcspontok az

A D

oldalegyenesnek ugyanazon a partján helyezkednek el, az

A

E

F

és

D

pontok valóban egy körön vannak, mégpedig az

A D

szakasz egyik

{22, 5}^{\circ}

-os látókörívén. Ezzel az első állítást bizonyítottuk.
Az

A E F D

húrnégyszögben

D

szög derékszög, a szemközti

E

csúcsnál levő szöge is derékszög, ezért

A E K H

(konvex) négyszög is húrnégyszög.

C E B ∢ = A E B ∢

E D

egyenesre vonatkozó tengelyes szimmetria miatt, ezért

A E C ∢ = A E H ∢ = 45^{\circ}

. Ekkor viszont

A K H ∢

45^{\circ}

-os, mivel

A E K H

húrnégyszögben az

A H

oldal

K

-ból ugyanakkora szög alatt látszik, mint

E

-ből. Így az

A K H

derékszögű háromszögben

H A K ∢ = 45^{\circ}

.
Az

A C

szakasz az

A H

félegyenessel szintén

45^{\circ}

-os szöget alkot, mégpedig ugyanabban a félsíkban, mint

A K

, ezért

C

rajta van az

A K

egyenesen.

Józsa Miklós (Sátoraljaújhely, Kossuth L. Gimn., III. o. t.)