Feladat: 1452. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: -
Füzet: 1974/január, 16 - 18. oldal  PDF  |  MathML 
Témakör(ök): Egyenlő szárú háromszögek geometriája, Indirekt bizonyítási mód, Kombinatorikus geometria síkban, Testek szinezése, Gyakorlat
Hivatkozás(ok):Feladatok: 1973/január: 1452. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Kíséreljük meg ellenpéldát adni az állításra, vagyis az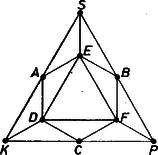
A, B, ..., F pontokat azzal a kiegészítő követelménnyel kiszínezni, hogy a tíz kis háromszög egyikének se legyen mind a három csúcsa más-más színű. Azt fogjuk belátni, hogy ez nem lehetséges, és ez fogja bizonyítani a feladat állítását.

 

 

1. ábra
 

A kiegészítő követelmény ‐ másképpen: az állítással való szembehelyezkedés ‐ célszerű lesz. Ugyanis az eredeti előírás csak csekély korlátozást jelent a színezésben (csupán az oldalfelező pontok részére zár ki egy-egy színt), vagyis megfordítva: sok lehetőséget enged a színek választásában; de főleg azért, mert sok munkát ígér avval, hogy minden egyes színezés végeztével addig kell ellenőriznünk kis háromszögeit, míg találunk köztük egy, az állítás szerint létező ,,háromszínű'' háromszöget. A kiegészítő követelményt viszont már a színezés folyamán, az ábra részleteiben érvényre lehet juttatni, sőt éppen azt várjuk, hogy így egyetlen színezést sem lehet majd befejezni; nem végzünk tehát hiábavaló munkát, vagy legalábbis kevesebbet.
A kiegészítő követelmény melletti színezés lehetetlen volta néhány háromszög megfelelő színezése után abból fog kiütközni, hogy az utolsónak (vagy mások után) színezendő pont számára a benne összefutó háromszögek egyike-másika tiltja egyik-egyik szín alkalmazását, és több ilyen háromszög együttesen mind a 3 színt letiltja.
Az oldalfelező pontok lényegében kétféleképpen színezhetők:
I. együttvéve két színnel, ha ti. a háromszög valamelyik csúcsának színét mindkét onnan kifutó oldal felezőpontja örökli, a szemben levő oldal felezőpontja pedig a további két szín egyike;
II. úgy, hogy A, B, C mindegyike más színű.
Az I. lehetőségre példa, ha A=S=B és C=K (röviden az egyenlőség jelével rendeljük hozzá a ponthoz a szín kezdőbetűjét, 2. ábra).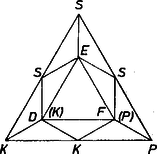
 

 

2. ábra
 

Minden más ilyen, azaz 2 színt használó lehetőség visszavezethető erre, az ábra 120∘-os elfordításával vagy tengelyes tükrözésével. Ugyanis nem változtat a feladaton, ha az ABC és DEF háromszögeket szabályosaknak tekintjük, a többieket egyenlő szárúaknak, hiszen a követelmények szempontjából nem lényeges, hogy a megindulásban hol van a K, a P, az S csúcs, helyettük akár X, Y, Z színt vagy akár három különböző jelet is írhatnánk. Ezt röviden így mondjuk: a feladat szimmetriái alapján elég a választott példával foglalkoznunk; itt szimmetrián tágabb értelemben a színek egyenrangúságát is értjük.
A 2. ábrán az F pont az FPK háromszög miatt nem lehet S, különben a háromszög háromszínű lenne; továbbá hasonlóan F az FPS háromszög miatt K sem lehet, tehát arra kényszerítettük magunkat, hogy F-et P-re fessük. Folytatólag a DFK=DPK háromszög miatt D≠S, a DKS háromszög miatt D≠P, tehát egyedül D=K lehetséges. Így pedig E a ESD=ESK, EDF=EKP és EFS=EPS háromszögek egyidejű figyelembevételével az előzetes megjegyzés szerint színezhetetlen.
Az oldalfelező pontok II. típusú színezése mellett A színe meghatározza B-ét, majd C-ét is (vagy előbb a C-ét, utána a B-ét), a szimmetria alapján elég az A=K, B=S, C=P esettel foglalkozunk (3. ábra, itt a még meglevő forgási szimmetria miatt kissé lassabban jutunk előre).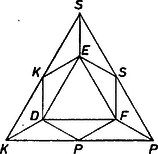
 

 

3. ábra
 

Az EKS háromszög miatt E≠P. Ha E=K volna, akkor az EFS=KFS háromszög miatti F≠P, és az FSP háromszög miatti F≠K letiltásból F=S következnék, és D színezhetetlenné válna a DKP, DPF=DPS, DFE=DSK háromszögek miatt. Eszerint már csak E=S-től remélhető megoldás. A színek szimmetriáját felhasználva ugyanígy kapjuk azt, hogy csak F=P és D=K lehetséges, így pedig a DEF háromszög háromszínű.
Ezzel az előrebocsátottak szerint a feladat állítását bebizonyítottuk.
 

II. megoldás. Hosszabbnak ígérkezik a színezést a teljesen szabad D, E, F pontokkal kezdeni, mégis rövidebben érünk célhoz, egyszerűbben ütközünk bele A, B vagy C színezhetetlenségébe. ‐ Az I. megoldáshoz hasonlóan itt sem engedünk meg háromszínű háromszöget, vagyis minden kis háromszögben megkövetelünk legalább egy szín-ismétlődést.
Mivel a DEF háromszög szimmetrikusan fekszik a KSP háromszöghöz képest, és a színek eddigi felhasználásuk szerint is egyenrangúak (mindegyik színnel 1 pont), azért a DEF háromszögben ismétlődő színnek bármelyiket választhatjuk, legyen ez K. Erre azonban nem festhetők együtt E és F, mert így (1. ábra) a SEB=SKB és a PFB=PKB háromszögek miatt B≠P és B≠S, holott B színének a feladat követelménye szerint vagy P-nek vágy S-nek kellene lennie. (Eddig D szóba sem jött, tehát lehetetlen a D=E=F=K színezés is.)
Így D-nek kell kéknek lennie, továbbá E és F egyikének. D=K alapján az ábra a K szín szempontjából szimmetrikus a KB tengelyre, ezért elég E=K-val próbálkozni. Ekkor a SEB=SKB háromszögből B≠P, tehát az eredeti követelmény szerint B=S; az FBE=FSK és FBP=FSP háromszögekből F=S; végül a CPF=CPS és CDF=CKS háromszögekből C nem festhető egyik előírt színére sem. Nem lehet tehát mindegyik pontot színezni, ha nem engedünk meg háromszínű háromszöget.
 

III. megoldás. A feladat állítását indirekt úton igazoljuk. Tegyük fel, hogy van olyan színezés, amikor nincs olyan kis háromszög, amelynek mind a három csúcsa különböző színű. Nevezzük PK oldalnak egy háromszög olyan oldalát, amelynek egyik végpontja piros, a másik kék. Számoljuk le kétféleképpen a PK oldalakat úgy, hogy mindegyiket annyiszor vegyük számításba, ahányszor fellép valamelyik kis háromszög oldalaként.
a) A PK oldalak száma páros, hiszen ha egy kis háromszögnek van PK oldala, akkor pontosan két ilyen oldala van, mert ekkor csúcsainak színezése vagy P, P, K vagy P, K, K. b) A PK oldalak száma páratlan, mert a nagy háromszög kerületén pontosan egy PK oldal van, és belsejében minden PK oldal pontosan két háromszög révén jön számításba.
A kapott ellentmondás azt bizonyítja, hogy mindig van legalább egy olyan kis háromszög, amelynek mind a három csúcsa különböző színű.
 

Megjegyzés. Az elmondott gondolatmenet alkalmazásával a feladat sokkal általánosabb feltételek mellett is megoldható, lásd a pontversenyen kívüli P. 180. probléma később közlendő megoldását.