Feladat: 1436. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1973/március, 116 - 118. oldal  PDF  |  MathML 
Témakör(ök): Tengelyes tükrözés, Szögfelező egyenes, Rombuszok, Téglalapok, Deltoidok, Húrnégyszögek, Négyszögek geometriája, Gyakorlat
Hivatkozás(ok):Feladatok: 1972/október: 1436. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen az ABCD=N deltoid szimmetriatengelye BD, erre a keletkezett EFGH négyszög is szimmetrikus, ahol E az OA, OB egyenesekre állított merőlegesek metszéspontja s i. t., O pedig a beírt kör középpontja, természetesen ez is a BD egyenesen van (1. ábra).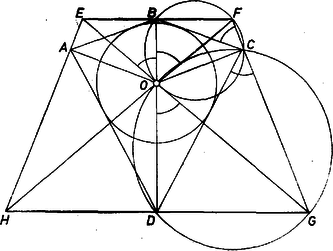

 

 

1. ábra
 
 

Elég azt megmutatni, hogy az EG átló átmegy O-n (hiszen ekkor tükörképe, az FH átló is átmegy rajta).
A CO félegyenes felezi a BCD szöget, tehát CO-n tükrözve CB és CD egymásba mennek át, az új négyszög FG oldalegyenese pedig önmagába. Másrészt az OBFC és OCGD négyszögek húrnégyszögek, mert szemben fekvő B és C, ill. C és D csúcsaiknál derékszögek vannak. Így a tengelyes szimmetriák, valamint a kerületi szögek tétele alapján
EOB∢=FOB∢=FCB∢=GCD∢=GOD∢.**
Az utolsó szög forgási iránya egyező az elsőével, mert a kétszeri tükrözés (* jelek a megfelelő egyenlőségi jel alatt) visszaállítja az eredeti irányt. S mivel OD az OB-nek 180∘-kal való elfordítottja, azért OG is 180∘-kal való elfordítással áll elő OE-ből, tehát E, O, G valóban egy egyenes pontjai.
Megjegyezzük még, hogy ha N-ben speciálisan AB=AD is fennáll, vagyis N rombusz, tehát AC is szimmetriatengely, és O ezen is rajta van, akkor az EFGH négyszög téglalap, és az állítás nyilvánvaló (2. ábra).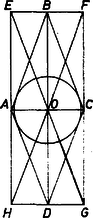
 

 

2. ábra
 

 

Megjegyzés. A deltoid konvex voltát abban használtuk fel, hogy használtuk a beírt kör O középpontját. Konkáv deltoidba ugyanis nem lehet kört beleírni.
 

II. megoldás. Az I. megoldásban bevezetett betűzést tovább használjuk. Azt, hogy az E, G és O pontok egy egyenesbe esnek, azzal mutatjuk meg, hogy mindhárom pont egyenlő távolságra van N-nek szemben fekvő AD és BC oldalegyeneseitől, éspedig az AD, BC egyenespár egyik szögfelező félegyenesén vannak rajta, ha ezek metszik egymást, illetve a középpárhuzamosukon, ha AD∥BC. A bizonyítás során nem fogjuk felhasználni, hogy deltoidból indultunk ki, csak azt, hogy van olyan kör, mely a konvex N négyszög mindegyik oldalát érinti. Ebből következik, hogy az állítás érvényes bármely konvex érintőnégyszögből az előírás szerint előállított négyszög átlóira.
Az új négyszög csúcsai mindig létrejönnek, mert az OA-ra A-ban és OB-re B-ben állított merőleges csak akkor nem metszi egymást, ha A, O, B egy egyenesen vannak, ekkor viszont O nincs benne N-ben, hanem a kerületén van.
Az N csúcsait O-val összekötő egyenesek felezik N belső szögeit, ezért az EFGH négyszög oldalegyenesei felezik N külső szögeit, hiszen egy szög felezőjére a csúcsában állított merőleges felezi a szög mellékszögeit.
 

Eszerint E mint az EH és EF külső szögfelezők metszéspontja egyenlő távolságra van egyrészt AB-től és AD-től, másrészt BA-tól és BC-től, tehát (AB közvetítésével) az AD, BC egyenespár tagjaitól, és ezeknek azon a partján van E, mint az eredeti négyszög. A 3. ábrán E az ABK háromszögbe beírt kör középpontja, ahol K az AD, BC egyenespár metszéspontja, AB-nek az N-et nem tartalmazó oldalán.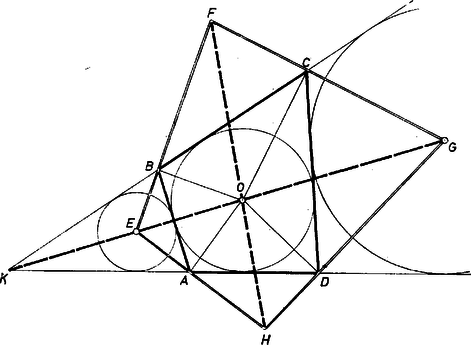
 

 

3. ábra
 
 

Hasonlóan a G pont GH révén egyenlő távolságra van DC-től és DA-tól, GF révén pedig CD-től és CB-től, tehát DA-tól és CB-től mért távolságai egyenlők, és G mindkét egyenesnek azon a partján van, mint N. G a CDK háromszög CD oldalához hozzáírt külső érintő kör középpontja.
Végül O az N-nek mind a négy oldalegyenesétől egyenlő távolságra van és benne van N-ben. Ezek szerint E, G és O rajta vannak az ABK háromszög AKB szögének belső felezőjén, és ezzel állításunkat bebizonyítottuk. Bizonyításunk a betűk kellő cseréjével az FH átlóra is érvényes. ‐ Ezzel a feladatot megoldottuk. Egyszersmind azt is kaptuk, hogy az EG, FH átlóknak egyszerű jelentésük van N-re vonatkozóan.