Kezdőlap


Feladat:	1383. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1972/szeptember, 16 - 18. oldal		PDF \| MathML
Témakör(ök):	Derékszögű háromszögek geometriája, Síkbeli ponthalmazok távolsága, Síkgeometriai számítások trigonometria nélkül háromszögekben, Diszkusszió, Gyakorlat
Hivatkozás(ok):	Feladatok: 1971/október: 1383. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Megmutatjuk, hogy az adott $A B C = H$ szabályos háromszög belsejében kétféleképpen lehet kijelölni a feladat első mondata szerinti három pontot. Ebből mindjárt adódik a kérdés magyarázatául, hogy a két tanuló a két különböző ponthármasbeli távolságokat adta meg; csak azt kell majd még belátnunk, hogy a két ponthármas által meghatározott távolságok különböznek egymástól.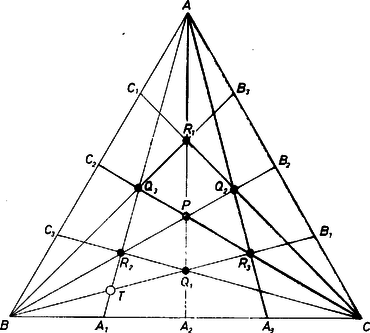
Rajzoljuk meg a $B A C,$ $C B A,$ $A C B$ szöget negyedelő egyeneseket és jelöljük a szemben levő $B C,$ $C A,$ $A B$ oldallal való metszéspontokat az $A$ , $B$ , $C$ forgási irány szerint rendre $A_{i}$ -vel, $B_{i}$ -vel, $C_{i}$ vel $(i = 1, 2, 3)$ .

A keresett ponthármas pontjait a

H

csúcsaival összekötő egyenesek csak e 9 egyenes közül valók lehetnek, tehát csak olyan pontok jöhetnek szóba, amelyeken három ilyen szögnegyedelő megy át. Vannak ilyen pontok, hiszen

A A_{2}

B B_{2}

C C_{2}

H

szimmetriatengelyei és mindegyik tengelyre vonatkozóan a többi negyedelők tükrös párokat alkotnak, és így a tengelyen metszik egymást. Az

A A_{2}

tengelyen van a

B B_{1}

C C_{3}

pár, a

B B_{2}

C C_{2}

pár és a

B B_{3}

C C_{1}

pár metszéspontja, jelöljük ezeket rendre

Q_{1}

-gyel,

P

-vel,

R_{1}

-gyel. Hasonlóan kapjuk a

B B_{2}

tengelyen a

Q_{2}

P

R_{2}

és a

C C_{2}

-n a

Q_{3}

P

R_{3}

a hármas metszéspontokat.
E 7 ponttal felsoroltuk a szögnegyedelők összes hármas metszéspontját. Elég belátni ehhez a szimmetriák alapján azt, hogy valamelyik szélső negyedelőn, pl.

A A_{1}

-en nincs további hármas metszéspont. A rajta eddig megállapított

R_{2}

-t és

Q_{3}

-at

B

-vel összekötő egyenes a

B B_{2}

, ill.

B B_{3}

, így a

B

-ből induló negyedelők közül már csak a

B B_{1}

-gyel való

T

metszéspontja jöhet szóba. Ez azonban

B B_{1}

-nek az

A B

és

A A_{2}

közti

B Q_{1}

, szakaszán van mint belső pont, ezért

B C T ∢ < B C Q_{1} ∢ = 15^{\circ}

, tehát

T

-n nem megy át negyedelője az

A C B

szögnek; ezt akartuk belátni.
A talált 7 hármas metszéspont mindegyike rajta van a H valamelyik tengelyén,

P

pedig mind a három tengelyen rajta van. Így

P

semelyik

Q_{i}

-vel vagy

R_{i}

-vel

(i = 1, 2, 3)

nem tartozhat egy, a feladat szerinti ponthármasba, különben a ponthármast

A

-val,

B

-vel,

C

-vel összekötve nem kapnánk meg

H

-nak mind a 9 szögnegyedelőjét, pl. ha

P

Q_{1}

-gyel tartozna egy ponthármasba, akkor vagy

A A_{1}

- et vagy

A A_{3}

-at nem kapnánk meg.
Hasonlóan adódik, hogy

Q_{1}

nem tartozhat egy ponthármasba sem

R_{1}

-gyel (

A A_{2}

miatt), sem

R_{2}

-vel, sem

R_{3}

-mal (

C C_{3}

, ill.

B B_{1}

miatt). A

Q_{1}

Q_{2}

Q_{3} = H_{q}

ponthármas viszont előállítja

H

-nak mind a 9 szögnegyedelőjét. Ugyanígy kapjuk az

R_{1}

R_{2}

R_{3} = H_{r}

hármast és azt, hogy több megfelelő ponthármas nem állítható össze a 7 hármas metszéspont közül. Ezzel a megoldás elején kimondott állítást bebizonyítottuk. A

H

-nak

P

körüli 120

°

-os forgási szimmetriájából az is következik, hogy mind a

H_{q}

, mind a

H_{r}

ponthármasok egy-egy szabályos háromszög csúcsai.

2. Áttérve az előre jelzett számításra, a

H_{q}

H_{r}

szabályos háromszögeknek csak egy oldalát kell kiszámítanunk. Ezek egyenlők a köréjük írt kör

P Q_{1}

, ill.

P R_{1}

sugarának

\sqrt[]{3}

-szorosával.

P Q_{1}

, a

P B A_{2}

derékszögű háromszögben a

B

-nél levő szög felezőjével kettévágott

P A_{2}

oldalnak része, és e háromszög oldalai

B A_{2} = 1 / 2

A_{2} P = A A_{2} / 3 = \sqrt[]{3 / 6}

és

P B = 2 A A_{2} / 3 = \sqrt[]{3} / 3

.
Ezért

\begin{matrix} P Q_{1} : Q_{1} A_{2} = P B : A_{2} B, \end{matrix}

\begin{matrix} P Q_{1} : (P Q_{1} + Q_{1} A_{2}) = P Q_{1} : P A_{2} = P B : (P B + A_{2} B), \end{matrix}

\begin{matrix} P Q_{1} = P A_{2} \frac{P B}{P B + A_{2} B} = \frac{2}{\sqrt[]{3}} - 1. \end{matrix}

B C R_{1}

a szerkesztés szerint egyenlő szárú derékszögű háromszög, így

\begin{matrix} P R_{1} = A_{2} R_{1} - A_{2} P = B A_{2} - A_{2} P = \frac{1}{2} - \frac{\sqrt[]{3}}{6} . \end{matrix}

Ezekből az előre bocsátottak alapján

\begin{matrix} Q_{1} Q_{2} = \sqrt[]{3} \cdot P Q_{1} = 2 - \sqrt[]{3} (= 0, 268), \end{matrix}

\begin{matrix} R_{1} R_{2} = \sqrt[]{3} \cdot P R_{1} = \frac{\sqrt[]{3}}{2} - \frac{1}{2} (= 0, 366), \end{matrix}

és eredményeink igazolják a megoldás elején a kérdés magyarázatára közölt elgondolásunkat.

Megjegyzés. Ha a feladat nem kérdezte volna a lehetséges számeredményeket, akkor a 2. pont helyett elég lett volna ezt mondanunk:

H_{q}

és

H_{r}

háromszögek oldalainak aránya a nyilvánvalóan hasonló

A Q_{3} Q_{2}

és

A R_{2} R_{3}

háromszögekből

\begin{matrix} \frac{Q_{3} Q_{2}}{R_{2} R_{3}} = \frac{A Q_{3}}{A R_{2}} < 1, \end{matrix}

mert

Q_{3}

benne van az

A B P

háromszögben,

A Q_{3}

része az

A R_{2}

-nek, tehát

Q_{3} Q_{2} \neq R_{2} R_{3}