Kezdőlap


Feladat:	1382. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Hidvégi Attila , Katona Klára , Wettstein József
Füzet:	1973/december, 207 - 208. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Derékszögű háromszögek geometriája, Súlyvonal, Súlypont, Trapézok, Helyvektorok, Gyakorlat
Hivatkozás(ok):	Feladatok: 1971/október: 1382. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás.A $B A C = α$ szög a szerkesztés szerint megismétlődik a $B A C_{1}$ $C B A_{1}$ és $A C B_{1}$ szögekben, ugyanígy az $A B C = β$ szög az $A B C_{1}$ , $B C A_{1}$ és $C A B_{1}$ szögekben. Ezért egyrészt $C B_{1}$ is, $C A_{1}$ is párhuzamos $A B$ -vel a váltószögek alapján, tehát $C$ rajta van az $A_{1} B_{1}$ egyenesen, másrészt $B A B_{1} ∢ = A B A_{1} ∢ = α + β$ . Így pedig az $A B A_{1} B_{1}$ négyszög szimmetrikus trapéz (tekintet nélkül az eredeti $A C B$ szög nagyságára, az 1. ábrán már nem is derékszöget rajzoltunk $C$ -nél), másrészt $C_{1}$ a $C$ tükörképe az $A B$ egyenesre nézve, tehát $C C_{1}$ merőleges az $A B$ -re.
Legyen az $A B$ , $A_{1} B_{1}$ alap felezőpontja $F$ , ill. $F_{1}$ , és messe az $A B C$ háromszög $C F$ súlyvonala az $A_{1} B_{1} C_{1}$ háromszög $C_{1} F_{1}$ súlyvonalát $M$ -ben. Ekkor $F F_{1}$ a trapéz tengelye, merőleges $A B$ -re, tehát párhuzamos $C C_{1}$ gyel, és $F F_{1} = C_{0} C$ ‐ ahol $C_{0}$ a $C$ vetülete $A B$ -n, ‐ és $C_{1} C = 2 C_{0} C = 2 F F_{1}$ Ezek szerint a $C C_{1} M$ háromszög az $F F_{1} M$ háromszögnek $2$ -szeresre nagyított képe $M$ -ből mint centrumból, $M C = 2 M F$ , és $M C_{1} = 2 M F_{1}$ tehát $M$ úgy harmadolja a $C F$ $C_{1} F_{1}$ súlyvonalakat, hogy a kétszeres rész a csúcs felé esik. Így pedig $M$ mindkét háromszögnek súlypontja, az állítást bebizonyítottuk.
Ha az $A B C$ háromszögben $α = β$ , vagyis $C A = C B$ , akkor $C A_{1} = C B_{1}$ , és $F_{1}$ azonos $C$ -vel, $F$ pedig $C_{0}$ -lal, $M$ -ről nem beszélhetünk. Ekkor a súlypontokat rendre $S$ -sel, $S_{1}$ -gyel jelölve, mindkettő a $C C_{1}$ egyenesen van és $C S = \frac{2}{3} C C_{0} = \frac{1}{3} C C_{1} = C S_{1}$ , tehát $S_{1}$ azonos $S$ -sel.
Nem használtuk fel, hogy az $A C B$ szög derékszög, az összegről is csak azt, hogy kisebb $180^{\circ}$ -nál, ennélfogva az állítás minden háromszögre érvényes.

Hídvégi Attila (Budapest, Fazekas M. Gyak. Gimn.)

Wettstein József (Budapest, Piarista Gimn.)

Megjegyzés. Vegyük észre az utoljára kimondott általánosítással kapcsolatban, hogy a betűzésben látható szimmetria ellenére az állításban a

C

betű megkülönböztetett szerepet játszik; másképpen:

A

és

B

kiemelt szerepet kapnak mindjárt azzal, hogy az

A B C_{1}

és

A B C

háromszögek úgy hasonlók, hogy

A

-nak is,

B

-nek is önmaga felel meg, viszont

C

-nek ne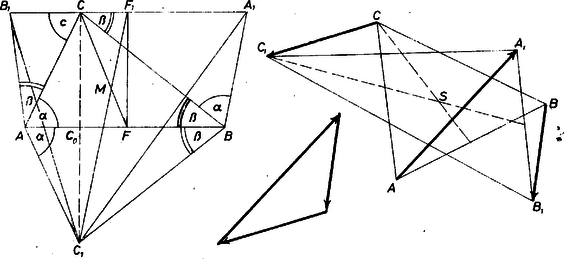m.

1. ábra 2. ábra

II. megoldás. Egy tetszőleges

A B C

háromszög

S

súlypontja akkor és csak akkor súlypontja egyszersmind az ugyanazon síkban fekvő

A_{1} B_{1} C_{1}

háromszögnek is, ha

\begin{matrix} \vec{S A_{1}} + \vec{S B_{1}} + \vec{S C_{1}} = \vec{0} \end{matrix}

(a zérusvektor). Mármost mindenesetre

\begin{matrix} \vec{A A_{1}} = \vec{A S} + \vec{S A_{1}}, \vec{B B_{1}} = \vec{B S} + \vec{S B_{1}}, \vec{C C_{1}} = \vec{C S} + \vec{S C_{1}} \end{matrix}

(1)

és

S

definíciója szerint

\begin{matrix} \vec{S A} + \vec{S B} + \vec{S C} = \vec{0}, azaz \vec{A S} + \vec{B S} + \vec{C S} = \vec{0} . \end{matrix}

Így (1)-ből összeadással a súlypont közös voltának szükséges és elegendő föltétele, kizárólag a háromszögek csúcsai alapján (2. ábra):

\begin{matrix} \vec{A A_{1}} + \vec{B B_{1}} + \vec{C C_{1}} = \vec{0} . \end{matrix}

Ezt célunknak megfelelően az alábbiak szerint alakítjuk:

\begin{matrix} \vec{A A_{1}} + \vec{A_{1} B} = \vec{A B} és \vec{B B_{1}} + \vec{B_{1} A} = \vec{B A} \end{matrix}

összeadásával

\begin{matrix} \vec{A A_{1}} + \vec{B B_{1}} + (\vec{A_{1} B} + \vec{B_{1} A}) = \vec{0} . \end{matrix}

tehát teljesülnie kell a következőnek:

\begin{matrix} \vec{C C_{1}} = \vec{A_{1} B} + \vec{B_{1} A}, \end{matrix}

és ez az I. megoldásban mondottak szerint teljesül is.

Katona Klára (Budapest, Fazekas M. Gyak. Gimn., I. o. t.)