Kezdőlap


Feladat:	1329. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bacsó G. , Bálint L. , Bodnár I. , Boros E. , Császár Gy. , Éber N. , Filep J. , Fűzy Cs. , Füredi Z. , Földes T. , Gál P. , Győri E. , Hanák G. , Kelen M. , Komornik V. , Koppány I. , Major T. , Nagy Z. , Oláh Vera , Párkány Katalin , Pataki B. , Pintér I. , Pipek J. , Sándor T. , Somogyi B. , Szász Gy. , Szeredi J.
Füzet:	1972/április, 157 - 158. oldal		PDF \| MathML
Témakör(ök):	Magasságvonal, Szögfelező egyenes, Beírt kör, Hozzáírt körök, Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1970/október: 1329. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Legyenek a mondott $E$ , $F$ , $G$ , $H$ pontok az $A B C$ háromszög $B C$ oldalegyenesén és jelöljük a háromszög oldalait szokás szerint $a$ , $b$ , $c$ betű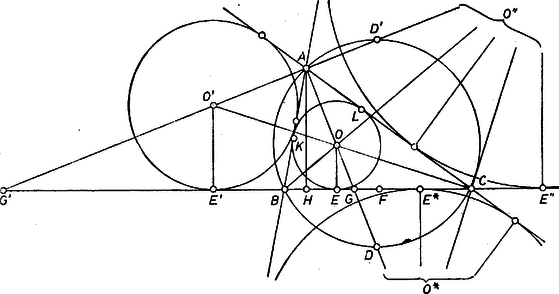vel.

Válasszuk úgy a betűzést, hogy

A B = c < A C = b

(ugyanis

b = c

esetén a 4 pont egybeesik, az állítás semmitmondó). Föltevésünk mellett viszont a 4 pont különböző egymástól ‐ az állításbeli 4 szakasz egyike sem 0 ‐, és a pontok sorrendje is egyértelmű. Ugyanis mivel az

A

csúcs ‐ és vele

H

is ‐ az

F

-ben emelt

f

merőlegesnek

B

-t tartalmazó partján van, azért ott van

E

és

G

is, mert az

A

-beli szögfelező átmegy

f

és a háromszög köré írt kör

A

-t nem tartalmazó

B C

ívének

D

felezőpontján, és

G

, valamint a beírt kör

O

középpontja az

A D

húron van; és mivel még

D G < D O < D A

, azért

F G < F E < F H

, tehát a pontok sorrendje

C

F

G

E

H

B

; a

H

pont egybeesik

B

-vel, ill. túlesik rajta, ha

C B A ∢ \geq 90^{\circ}

.
Ezek alapján a négy pontnak

B

-től mért távolságaiból az állításbeli négy szakasz hossza kiszámítható. Mindjárt elsőnek

B F = a / 2

. A szögfelező osztási aránya alapján

B G = a c / (b + c)

. A beírt körhöz a csúcsokból húzott érintőszakaszok egyenlősége alapján, a kör,

A B

-n levő

K

és

A C

-n levő

L

érintési pontját is felhasználva

\begin{matrix} B E = \frac{B K + B E}{2} = \frac{B A + B C - (A L + C L)}{2} = \frac{c + a - b}{2} . \end{matrix}

Végül az

A H B

és

A H C

derékszögű háromszögek közös befogójára,

B H = x

jelöléssel, fennáll

\begin{matrix} A H^{2} = A B^{2} - B H^{2} = A C^{2} - C H^{2}, c^{2} - x^{2} = b^{2} - {(a \mp x)}^{2}, \\ x = \pm \frac{a^{2} - b^{2} + c^{2}}{2 a} \end{matrix}

(az alsó előjelek akkor érvényesek, ha

C B A ∢ > 90^{\circ})

.
Ezekből kivonással,

H

esetében

B H

irányát is figyelembe véve:

\begin{matrix} E G & = B G - B E = \frac{(b - c) (b + c - a)}{2 (b + c)}, \\ F H & = B F \mp B H = \frac{(b - c) (b + c)}{2 a}, \\ E F & = B F - B E = \frac{b - c}{2}, \\ E H & = B E \mp B H = \frac{(b - c) (b + c - a)}{2 a}, \end{matrix}

és tüstént látjuk, hogy a felső két kifejezés szorzata egyenlő az alsó kettőével, az állítás helyes.

II. A hasonló összefüggések keresésében

E

helyén három külső érintő (hozzáírt) kör érintési pontja jön szóba, legyen ez a

B C

B A

C A

oldalhoz hozzáírt kör esetében rendre

E^{*}

E'

E''

. Közülük az első kör

O^{*}

középpontja ugyancsak az

A G

szögfelezőn van rajta, az utóbbiak

O'

O''

középpontja pedig a

B A C

szög külső szögeinek

A G'

felezőjén, tehát

G

-t csak az utóbbi két esetben pótoljuk

G'

-vel. Így a következő három összefüggés várható:

\begin{matrix} E^{*} G \cdot F H = E^{*} F \cdot E^{*} H, E' G' \cdot F H = E' F \cdot E' H, E'' G' \cdot F H = E'' F \cdot E'' H . \end{matrix}

(1)

A fentiekhez hasonlóan adódik, hogy új pontjaink sorrendje a

B C

egyenesen a következő:

G'

E'

B

és

H

a fentiek szerint,

F

E^{*}

C

E''

, valamint hogy az új pontok

B

-től mért távolságának abszolút értéke:

\begin{matrix} B G' = \frac{a c}{b - c}, B E' = \frac{b + c - a}{2}, B E^{*} = \frac{a + b - c}{2}, B E'' = \frac{a + b + c}{2} . \end{matrix}

Ezek alapján a fentihez hasonló számítás mutatja, hogy az (1) egyenlőségek mindegyike helyes.