| Feladat: | 1023. matematika gyakorlat | Korcsoport: 14-15 | Nehézségi fok: átlagos |
| Megoldó(k): | Andor Cs. , Bálványos Z. , Berács József , Bulkai T. , Csörgei J. , Lakner Mária , Mérő L. , Moson P. , Orbán G. , Sax Gyula , Szűcs A. , Takács J. , Tátray P. , Vályi I. | ||
| Füzet: | 1966/október, 71 - 73. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Tengelyes tükrözés, Egyenlő szárú háromszögek geometriája, Gyakorlat, Síkgeometriai számítások trigonometria nélkül | ||
| Hivatkozás(ok): | Feladatok: 1965/december: 1023. matematika gyakorlat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. Az háromszög -nál és -nél levő szöge , így . Legyen tükörképe -re (1. ábra), ekkor az szabályos, mert , és . Másrészt , mert -ből induló oldalaik egyenlők, továbbá , és , tehát . Eszerint az egyenlő szárú és , tehát az köré írt körön van. Így , amint a feladat állítja. 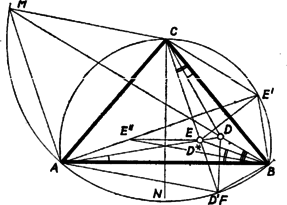 Tükrözzük az egyenest -re, és messe a képét a egyenes -ben. Ekkor az egyenlő oldalú, mert -nál és -nél -os szöge van, így . Eszerint a egyenlő szárú, , és , vagyis a egyenes -re vonatkozó tükörképén is rajta van, tehát azonos -nek -re való tükörképével. Ezért , a egyenlő oldalú, rajta van felező merőlegesén. Ugyanez áll -re is, így a egyenlő szárú háromszög szimmetriatengelye, felezi a szöget, tehát , ami a feladat első állítása. Megjegyzések. 1. A tükörképből kiindulva belátható, hogy a és a szabályos, utóbbi azért, mert -nál -os szöge van és a , feltételek ellentmondásra vezetnek. Így , mindkettő egyenlő szárú, a szárak közt -os szöggel. Másrészt a középponti és kerületi szögek összefüggése alapján belátható, hogy a középpontú, -n és -n átmenő körön van. Így , amiből következik, hogy az és egyenesek metszéspontja. Ezekből már következik a feladat mindkét állítása. 2. Mesterkéltebb, de egyszerűbb az ábra következő származtatása. Legyen a -ben és . Forgassuk ezt el körül -kal a helyzetbe úgy, hogy a belsejében legyen. Ekkor az is szabályos; továbbá és metszéspontját -vel jelölve -os csúcsszögű egyenlő szárú háromszög. Így az és a , pont teljesíti a feladat feltételeit, és nyilvánvalóan teljesülnek az állítások is. (Tusnády Gábor) 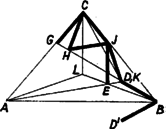 Messe az szimmetriatengelyét a egyenes az pontban. Ekkor az szögfelezője, és , így III. megoldás. A két állítást egymástól függetlenül bizonyítjuk. Az elsőhöz elég azt belátni, hogy . Ez igaz, ha ; ezt bizonyítjuk. Messe a egyenes a körül írt sugarú kört másodszer -ben (1. ábra). Ekkor , ezért egyenlő oldalú háromszög, továbbá . Így pedig , , és végül . A második állításhoz elég azt belátni, hogy negyedeli a szöget, vagy ami ugyanaz, felezi a szöget, ahol az szimmetriatengelye. Legyen tükörképe -re , -re . Ekkor , , vagyis felezi az szöget, és így . Másrészt, mint már láttuk, , ezért . a szög mindkét szárától fele ekkora távolságban van, tehát valóban felezi a szöget. Megjegyzés. bizonyításához segítségül vehetjük az alap fölé a -t tartalmazó partján szerkesztett egyenlő oldalú háromszög csúcsát is. Ekkor , , , így , . |