Kezdőlap


Feladat:	873. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Szentiványi Béla
Füzet:	1964/október, 54 - 56. oldal		PDF \| MathML
Témakör(ök):	Egyéb sokszögek hasonlósága, Húrnégyszögek, Gyakorlat, Síkgeometriai bizonyítások
Hivatkozás(ok):	Feladatok: 1963/november: 873. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen az $A B C D$ húrnégyszög köré írt kör egy pontja $M$ . Ha $M$ egybeesik egy csúccsal, az egyenlőség nyilvánvalóan helyes, mindkét oldalán 0 áll. Más esetben választhatjuk a betűzést úgy, hogy $M$ a $C$ , $D$ pontokat nem tartalmazó $A B$ körív belső pontja legyen.
Legyen $M$ vetülete az $A B, B C, C D, D A$ oldalegyenesen rendre $P, Q, R, S$ , és $M P = p$ , $M Q = q$ , $M R = r$ , $M S = s$ . Megmutatjuk, hogy az $M P A S$ és $M Q C R$ négyszögek hasonlók (1. ábra), csúcsaik a felsorolás rendjében felelnek meg egymásnak. Ha ez fennáll, akkor többek közt első és utolsó oldalaik aránya egyenlő:

\begin{matrix} p : s = q : r, \end{matrix}

ami egyértelmű a feladat állításával.
Két négyszög hasonló, ha bármelyik megfelelő átlójukkal háromszögekre bontva a rész‐háromszögek páronként hasonlók. Ez teljesül, ha egymás utáni szögeik egyenlők, továbbá egy‐egy megfelelő csúcsukban az átló a megfelelő oldalakkal egyenlő szögeket zár be, ‐ így ugyanis minden további megfelelő csúcspárban is fennáll az átló és az oldalak közti szögek egyenlősége.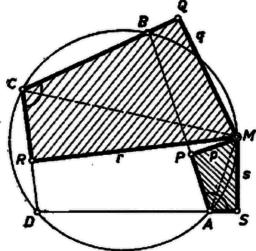

1. ábra

Az 1. ábrán a

P M S A

és

Q M R C

négyszögekben a

P

S

, ill. a

Q

R

csúcsnál derékszög van, az

A

-nál levő szög az

A B C D

négyszög külső szöge, a

C

-nél levő szög pedig az

A B C D

négyszögnek is szöge, így ezek is egyenlők, mert a négyszög húrnégyszög. Így a két négyszög

M

-nél levő szögei is egyenlők. Az előbbi meggondolást az

A M C D

húrnégyszögre ismételve

M A S ∢ = M C R ∢

, és így

M A P ∢ = M C Q ∢

.
Ezzel az állítást a bemutatott helyzet esetére bebizonyítottuk.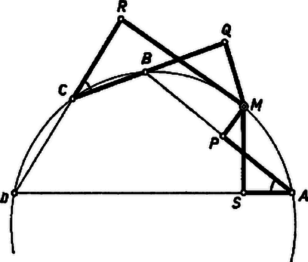

Szentiványi Béla (Budapest, Rákóczi F. g. II. o. t.)

2. ábra

Megjegyzés. A 2. ábra helyzetében az

M P A S

és az

M Q C R

négyszög hurkolt. A hasonlóság ezekre is fennáll. Itt a

M P A S

négyszög

P A S

szöge azonos az

A B C D

négyszög

B A D

szögével, viszont az

M Q C R

és

A B C D

négyszögek

C

-nél levő szögei kiegészítő szögek.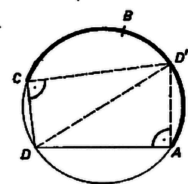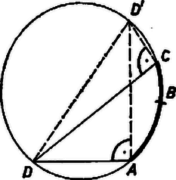

3. ábra

4. ábra

A fenti helyzetben is felhasználtuk, hogy a

P A S

és a

Q C R

szögek egyike az

A B C D

négyszögnek belső szöge, a másika pedig külső szög. Könnyű belátni, hogy nincs

M

számára olyan helyzet, hogy a mondott szögek mindegyike belső szög, sem olyan, hogy mindkettő külső szög. Ugyanis mialatt

M

-et

A

-tól

B

-ig mozgatjuk a

D

-t nem tartalmazó

A B

íven (3. ábra),

S

addig marad

A

-nak ugyanazon oldalán, míg

M

át nem lépi azt a

D'

pontot, ahol az

A D

-re

A

-ban emelt merőleges metszi a mondott ívet. Az is lehetséges, hogy

S

mindig ugyanazon oldalán adódik

A

-nak, ha ti.

D'

nem tartozik hozzá a mondott

A B

ívhez (4. ábra).

D'

D

-ből kiinduló átmérő végpontja, és itt metszi a kört a

C

-ben

D C

-re emelt merőleges is, ezért

R

szintén akkor lépi át

C

-t, amikor

M

átlépi

D'

-t, vagy pedig egyáltalán nem lépi át

C

-t. Állításunk most már közvetlenül belátható a 3‐4. ábrákról, amelyek

A

C

D

és

D'

kölcsönös helyzetének minden lehetséges típusát bemutatják (

A

és

C

ugyanis a vizsgált szempontból felcserélhetők); a

B

és

M

számára szóba jövő körív vastagon van rajzolva.
Ha végül

M

azonos

D'

-vel (5. ábra), akkor

S \equiv A

R \equiv C

Q R M ∢ = P S M ∢

, és a feladat állítása a

Q R M

és

P S M

derékszögű háromszögek hasonlóságából következik.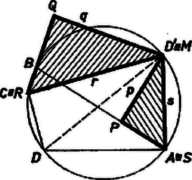

5. ábra