Kezdőlap


Feladat:	419. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Álmos Á. , Bartha L. , Bender Cecilia , Bognár L , Bóné A. , Börzsöny L. , Elbert Á. , Endrődy T. , Farkas Gy. , Fejes L. , Füle K. , Gaál S. , Garda Á. , Gergely Cs. , Grallert F. , Gyene A. , Győry Matild , Hadik Z. , Halász G. , Halász Gábor , Hites F. , Illés L. , K. Nagy Ildikó , Katona Gy. , Kaviák L. , Kolonits F. , Lassányi F. , Losonczy L. , Magos A. , Majsai L. , Majtényi S. , Mocskónyi M. , Muszély Gy. , Müller M. , Németh Marianne , Ortutay M. , Papp Éva , Raisz Klára , S. Nagy Erzsébet , Sikabonyi Gy. , Simonfai L. , Soós S. , Szabó Gy. , Szatmári A. , Szatmári G. , Tamás Gy. (Bp.) , Tatai P. , Trón L. , Újteleki Anna , Zahumenszki Zille , Zombori L.
Füzet:	1958/január, 8 - 9. oldal		PDF \| MathML
Témakör(ök):	Rombuszok, Diszkusszió, Négyszögek szerkesztése, Gyakorlat
Hivatkozás(ok):	Feladatok: 1957/április: 419. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az 1. ábrán megrajzoltuk a megszerkesztettnek képzelt $A B C D$ romb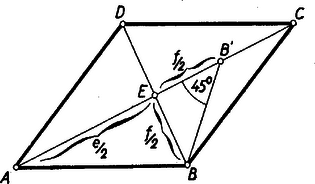uszt.

1. ábra

A rombusz egyik oldala és az átlók által alkotott

A E B

derékszögű háromszögből ismert az átfogó:

\frac{k}{4}

, és ismert a két befogó összege:

\frac{e + f}{2} = \frac{u}{2}

. Kérdés, hogyan lehet ebből az

A E B

derékszögű háromszöget megszerkeszteni.
Mérjük rá pl. a rövidebb félátlót,

E B

-t a hosszabbik meghosszabbítására. Az így kapott

A B' B

háromszögből ismert két oldala:

\frac{k}{4}

ill.

\frac{u}{2}

, és a

B' ∢ = 45^{\circ}

.
A szerkesztést ezek után a következő módon végezhetjük legegyszerűbben (2. ábra): Egy

A B' = \frac{u}{2}

hosszúságú szakaszra

B'

végpontjában

45^{\circ}

-os szöget mérünk, majd az

A

pontból a másik szögszárat

\frac{k}{4}

sugartú körívvel metsszük el, majd a

B

(és a

B_{1}

) metszéspontból merőlegest bocsátunk

A B'

-re, az így keletkező

A B E

és

A B_{1} E_{1}

háromszögek felelnek meg a feladat követelményeinek. A rombusz csúcsait ezután pl. úgy kaphatjuk, hogy az

E

csúcsra tükrözzük a háromszög másik két csúcsát.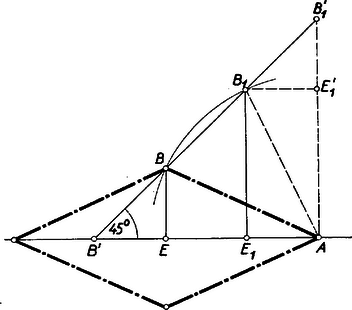

2. ábra

Csak látszólagos, hogy két megoldást kaptunk, mert belátható, hogy a kettő egybevágó. Állítsunk ugyanis

A B'

-re

A

-ban merőlegest, ez a

B' B

egyenest olyan

B'_{1}

pontban metszi, amelyre

A B'_{1} = A B'

B_{1}

-ből

A B'_{1}

-re a

B_{1} E'_{1}

merőlegest bocsátva az

A B E

és

A B_{1} E'_{1}

háromszögek egymás tükörképei az

A B' B'_{1}

, háromszög szimmetriatengelyére nézve,

A B_{1} E'_{1}

és

A B_{1} E_{1}

pedig egybevágók.
A feladat megoldhatóságának feltétele, hogy az

A

középpontú körívnek legyen a végpontoktól különböző közös pontja a

B' B'_{1}

szakasszal, azaz hogy

\begin{matrix} A B' > A B \geq \frac{\sqrt[]{2}}{2} A B', tehát \frac{u}{2} > \frac{k}{4} \geq \frac{\sqrt[]{2} u}{4}, \end{matrix}

vagy

\begin{matrix} \sqrt[]{2} u \leq k < 2 u . \end{matrix}

k = \sqrt[]{2} u

esetben speciális rombuszt: négyzetet kapunk. A

k = 2 u

esetben egy egyenesszakasszá lapul a rombusz.

Halász Gábor (Bp. II., Rákóczi g. II. o. t.)