Kezdőlap


Feladat:	402. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: könnyű
Megoldó(k):	Halász Gábor , Hornyánszky Tamás
Füzet:	1957/november, 119. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1957/február: 402. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A betűzést az ábra mutatja.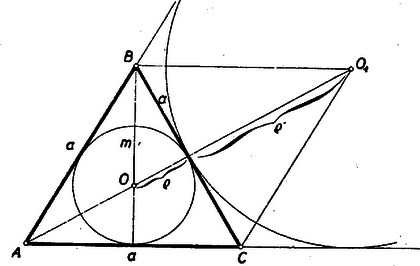

Egyenlő oldalú háromszögben a szögfelezők, a súlyvonalak és a magasságvonalak egybeesnek, és így

ϱ = \frac{m}{3}

.
Mivel a külső szögfelezők a belsőkre merőlegesek, és így a szemközti oldalakkal párhuzamosak, azért

A B O_{1} C

paralelogramma, vagyis

ϱ' = m

. Tehát

\begin{matrix} ϱ' (ϱ + ϱ') = m (\frac{m}{3} + m) = \frac{4 m^{2}}{3} = \frac{4}{3} {(\frac{a}{2} \sqrt[]{3})}^{2} = \frac{4}{3} \cdot \frac{3 a^{2}}{4} = a^{2}, \end{matrix}

ami bizonyítandó volt.

Halász Gábor (Bp. II., Rákóczi g. II. o. t.)

II. megoldás: Mivel az

A B O_{1} C

paralelogrammának két szomszédos oldala

A B = A C = a

, azért a paralelogramma rombusz, és így

B O_{1} = a

, és az átlók egymásra merőlegesek. A külső és belső szögfelezők merőlegesek egymásra, tehát az

O B O_{1 ▵}

derékszögű. Ismert tétel szerint a

B O_{1} = a

befogó mértani középarányos az egész átfogó

(O O_{1} = ϱ + ϱ')

és a befogónak az átfogón levő merőleges vetülete

(ϱ')

között, vagyis

\begin{matrix} a^{2} = (ϱ + ϱ') ϱ', \end{matrix}

ami bizonyítandó volt.

Hornyánszky Tamás (Bp. VIII.; Piarista g. I. o. t.)