Kezdőlap


Feladat:	F.2977	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bárász Mihály , Gyarmati Katalin , Kegyes Bálint , Kovács Baldvin , Maróti Gábor , Sánta Zsuzsa , Szobonya László , Valkó Benedek
Füzet:	1994/április, 206 - 208. oldal		PDF \| MathML
Témakör(ök):	Algebrai átalakítások, Ceva-tétel, Szögfelező egyenes, Számtani-mértani egyenlőtlenségek, Háromszög területe, Feladat
Hivatkozás(ok):	Feladatok: 1993/október: F.2977

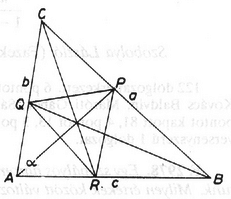
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Használjuk az ábra jelöléseit. Ismeretes, hogy a háromszög bármelyik szögfelezője a szög csúcsával szemközti oldalt a szöget bezáró oldalak arányában osztja. Ezért pl.

\begin{matrix} A Q = \frac{b \cdot c}{a + c}, A R = \frac{b \cdot c}{a + b} . \end{matrix}

Jelöljük pl. az

A Q R

háromszög területét

t_{A Q R}

-rel. A bizonyítandó állítás nyilván ekvivalens azzal, hogy

t_{A Q R} + t_{B P R} + t_{C P Q} \geq \frac{3}{4}

-t, amiből

\begin{matrix} \frac{t_{A Q R}}{t} + \frac{t_{B P R}}{t} + \frac{t_{C P Q}}{t} \leq \frac{3}{4} . \end{matrix}

A háromszögek területét két oldallal és a közbezárt szöggel kifejezve (2) bal oldalának első tagja így alakul:

\begin{matrix} \frac{t_{A Q R}}{t} = \frac{\frac{1}{2} \cdot \sqrt[]{\frac{b \cdot c}{a + b}} \cdot sin α}{\frac{1}{2} \cdot b \cdot c \cdot sin α} = \frac{b \cdot c}{(a + b) (a + c)} . \end{matrix}

Hasonlóan írhatjuk föl a (2) bal oldalán szereplő másik két tagot. Ezért a belátandó egyenlőtlenség:

\begin{matrix} \frac{b \cdot c}{(a + b) (a + c)} + \frac{a \cdot c}{(a + b) (b + c)} + \frac{a \cdot b}{(a + b) (b + c)} \geq \frac{3}{4} . \end{matrix}

A tötet eltávolítva és a szorzásokat elvégezve:

\begin{matrix} 4 (b c^{2} + b^{2} c + a^{2} c + a c^{2} + a b^{2} + a^{2} b) \leq \\ \leq 3 (a^{2} b + a b^{2} + a^{2} c + a c^{2} + b c^{2} + b^{2} c) + 6 a b c, \end{matrix}

amiből

\begin{matrix} \frac{b c^{2} + b^{2} c + a^{2} c + a c^{2} + a b^{2} + a^{2} b}{6} \geq a b c . \end{matrix}

a (3) számlálójában lévő 6 tag mértani közepe

\sqrt[6]{a^{6} b^{6} c^{6}} = a b c,

ezért (3) igaz. Egyenlőség pontosan akkor van, ha

a = b = c

. Mivel átalakításaink megfordíthatók, a feladat állítását megmutattuk.
Megjegyzés. Néhány megoldónk szögfelezők helyett a háromszög egy belső pontján áthaladó ‐ egyébként tetszőleges ‐

A P, B Q, C R

esetén is megmutatta, hogy

t_{P Q R} \leq \frac{t}{4}

. Ez a következőképpen történhet. Ha az

R

pont az

A B

oldalt

k : (1 - k)

arányban osztja, és hasonlóan

B P : P C = l : (1 - l)

, illetve

C Q : Q A = m : (1 - m)

, akkor a bizonyítandó állítás:

\begin{matrix} t - t \cdot k \cdot (1 - m) - t \cdot m \cdot (1 - l) - t \cdot l \cdot (1 - k) \leq \frac{t}{4}, \end{matrix}

és felhasználhatjuk, hogy a Ceva-tétel szerint

\begin{matrix} \frac{k}{1 - k} \cdot \frac{l}{1 - l} \cdot \frac{m}{1 - m} = 1. \end{matrix}

Szobolya László (Fazekas M. Főv. Gyak. Gimn., II. o.t.) dolgozata alapján