Kezdőlap


Feladat:	F.2973	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Arató Gabriella , Dienes Péter , Duzmath Zsolt , Galácz Ábel , Gergely Levente , Gyarmati Katalin , Halasi Zoltán , Izsák Ferenc , Jeszenszky Éva , Józsa Balázs Gábor , Király Csaba , Király Tamás , Koblinger Egmont , Lestyán Zsolt , Maróti Attila , Maróti Gábor , Nagy Vilmos , Németh Ákos , Németh Zoltán , Ódor Lajos , Perényi Márton , Rákóczi Bálint , Sánta Zsuzsa , Séllei Béla , Szádeczky-Kardoss Szabolcs , Szeredi Pál , Szeredi Tibor , Újváry-Menyhárt Mónika
Füzet:	1994/április, 202 - 204. oldal		PDF \| MathML
Témakör(ök):	Tengelyes tükrözés, Körülírt kör, Magasságpont, Terület, felszín, Húrsokszögek, Feladat
Hivatkozás(ok):	Feladatok: 1993/szeptember: F.2973

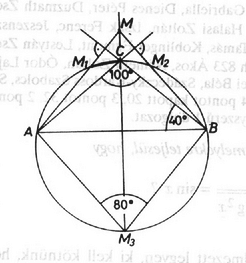
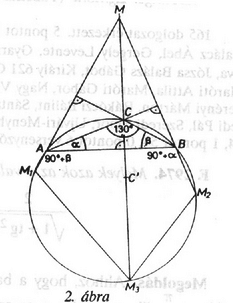
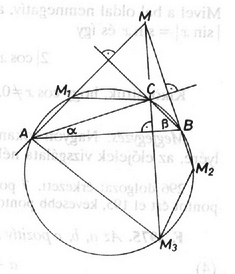
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ismeretes, hogy a háromszög magasságpontjának az oldalegyenesekre vonatkozó tükörképei a körülírt körön vannak. Ezért a feladatban szereplő konvex hatszög húrhatszög. Könnyen beláthatjuk, hogy ha a háromszög hegyesszögű, akkor a tükrözések után létrejövő húrhatszög területe éppen kétszerese a háromszög területének. Ha a háromszög derékszögű, akkor magasságpontja a derékszögű csúcs, amelynek a befogókra való tükörképe önmaga, tehát a feladatban említett hatszög nem jön létre. Ezért az eredeti háromszög tompaszögű. Legyenek ennek csúcsai $A, B, C,$ magasságpontja $M$ . Tegyük fel először, hogy $M$ -nek a tompaszöget bezáró oldalakra vonatkozó $M_{1}$ , illetve $M_{2}$ tükörképe az $M A$ , illetve $M B$ szakasz belső pontja (1. ábra). Világos, hogy az $A B M △$ magasságpontja $C$ , és ezért ez a háromszög hegyesszögű. A most vizsgált esetben a tükrözések után kapott hatszög: $M_{3} A M_{1} C M_{2} B$ , és előbbi megállapításunk szerint $A M B ∢ = A M_{3} B ∢$ hegyesszög, ezért a hatszög $80 \circ$ -os szöge $M_{3}$ -nál van. A szögek sorrendjéből azt is látjuk, hogy $M_{1}$ és $M_{2}$ -nél vannak a $140 \circ$ -os szögek. Az $A M_{3} B C$ húrnégyszögből $A C B ∢ = 100^{\circ},4,^{\circ}, 40^{\circ}$ , azaz a háromszög egyenlő szárú. De akkor a háromszög ─ és vele együtt a hatszög is ─ szimmetrikus az $M C$ egyenesre. A hatszög azonban, tekintve, hogy az $A$ és $B$ -nél lévő szögei különbözőek, nem szimmetrikus $M C$ -re, így ilyen megoldás nincs.
Másodszorra nézzük azt az esetet, amikor $M_{1}$ és $M_{2}$ az $M A$ -nak $A$ -n túli, illetve $M B$ -nek $B$ -n túli meghosszabbításán van (2. ábra). A hatszög csúcsai most

1. ábra 2. ábra

M_{3} M_{1} A C B M_{2}

sorrendben következnek. Az ábra jelölései szerint

M_{1} A B ∢ = 90^{\circ} + β

, ezért a hatszögben

M_{1} A C ∢ = 90^{\circ} + α + β .

Hasonlóan kapjuk, hogy

C B M_{2} ∢ = 90^{\circ} + α + β .

Ilyen hatszögben az

A

és

B

csúcsnál vannak egyenlő szögek, ezek a szögek

140^{\circ}

nagyságúak, amiért

α + β = 50 \circ

, és így

A C B ∢ = 130^{\circ}

. Ez valóban megoldás, mert az

M_{1} A C B M_{2}

körbe írt töröttvonal kiegészíthető a kívánt hatszöggé. Tükrözzük ugyanis

C

-t

A B

-re, a tükörkép legyen

C'

. Messe

C C'

a kört

M_{3}

-ban. Az

A C M_{3} M_{1}

húrnégyszögből

A M_{1} M_{2} ∢ = 90^{\circ} + α

, ezért

α = 20^{\circ}

esetén ez a szög

110^{\circ}

, és ugyanígy az

M_{2}

-nél lévő szög

120^{\circ}

. Ezután az

M_{3}

-nál lévő szög kiszámítható, ez

80^{\circ}

lesz. Mivel

C

-nek az

A B

-re vonatkozó tükörképe a

C M_{3}

szakasz belső pontja, a hatszög területe nagyobb lesz, mint a háromszög területének kétszerese.
Már csak az az eset van hátra, amikor

M_{1}

M A

belső pontja,

M_{2}

pedig

M B

meghosszabbításán van, vagy fordítva. (

M_{1}

vagy

M_{2}

nem eshet egybe

A

-val vagy

B

-vel, mert akkor nem jönne létre a hatszög.) Ekkor az

A B M_{2} ∢ = 90^{\circ} + α

, tehát tompaszög, és így az

A B M_{2} M_{3}

húrnégyszögben

M_{3}

-nál hegyesszög van (3. ábra). Ez a szög tehát a hatszög

80^{\circ}

-os szöge, és a feltételek szerint

M_{1} B C ∢ = 130^{\circ}, A M_{1} C ∢ = 140^{\circ} .

A B C M_{1}

húrnégyszögből

β = 40^{\circ}

, amiért

M_{1} A M_{3} ∢ = 100^{\circ}

, és ez ellentmondás, mert a hatszögnek nincsen

100^{\circ}

-os szöge. Ilyen ponthatos nem felelhet meg adatainknak. A feladat kérdésére tehát azt válaszolhatjuk, hogy a háromszög legnagyobb szöge

130^{\circ}

3. ábra

Koblinger Egmont (Fazekas M. Főv. Gyak. Gimn., III. o.t.) dolgozata alapján