Kezdőlap


Feladat:	F.2948	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Arató Gabriella , Csergőffy Tibor , Csörnyei Marianna , Dienes Péter , Dőtsch András , Futó Gábor , Gyarmati Katalin , Horváth Gábor , Imreh Csanád , K. L. , Kis Gábor , Maróti Attila , Megyesi Zoltán , Pete Gábor , Szeredi Tibor , Tichler Krisztián
Füzet:	1993/december, 504 - 505. oldal		PDF \| MathML
Témakör(ök):	Ceva-tétel, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1993/február: F.2948

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen az $A M$ és $B C$ egyenesek metszéspontja $P$ , és hasonlóan értelmezzük az ábrák $Q$ és $R$ pontja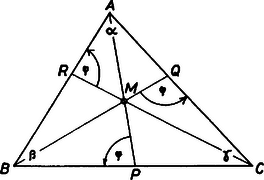it.

1. ábra

A feladat szövegében szereplő hajlásszögeket

φ

-vel jelöljük

(φ \leq 90^{\circ}) .

Könnyen látható, hogy a feltételnek kétféle ábra felelhet meg. Ha

φ = 90^{\circ}

, akkor készen vagyunk. Tegyük fel ezután, hogy az 1.ábra szerinti esetben

φ < 90^{\circ} .

Mivel

φ

külső szöge az

A Q B, B R C, C P A

háromszögeknek, ezért

α, β, γ < φ < 90^{\circ} .

Mindez azt jelenti, hogy az

A, B, C

csúcsokból induló magasságok rendre az

A B P, B C Q,

illetve

C A R

háromszögek belsejében haladnak. Ekkor azonban az

A

-ból, illetve

B

-ből kiinduló magasságok a

B M P

háromszög belsejében metszik egymást. Ezért, mivel a harmadik magasság a

C A R

háromszög belsejében halad, a háromszög három magasságvonala nem mehet át egy ponton. Ez ellentmondás, tehát

M

a háromszög magasságpontja.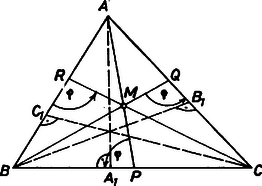

2. ábra

Tegyük fel ezután, hogy a 2. ábra szerinti esetben

φ \leq 90^{\circ}

. Az

A

-ból,

B

-ből és

C

-ből induló magasságvonalak talppontját

A_{1}

-gyel,

B_{1}

-gyel és

C_{1}

-gyel, a háromszög oldalait pedig a szokásos módon

a, b, c

-vel jelölve:

\begin{matrix} B P = B A_{1} + A_{1} P = c cos β + c sin β ctg φ, \\ P C = A_{1} C - A_{1} P = b cos γ - b sin γ ctg φ, \\ C Q = C B_{1} + B_{1} Q = a cos γ + a sin γ ctg φ, \\ Q A = B_{1} A - B_{1} Q = c cos α - c sin α ctg φ, \\ A R = A C_{1} - R C_{1} = b cos α - b sin α ctg φ, \\ R B = C_{1} B + R C_{1} = a cos β + a sin β ctg φ . \end{matrix}

Ceva tétele szerint

\begin{matrix} B P \cdot C Q \cdot A R = P C \cdot Q A \cdot R B, \end{matrix}

azaz

\begin{matrix} c (cos β + sin β ctg φ) a (cos γ + sin γ ctg φ) b (cos α - sin α ctg φ) = \\ = b (cos γ - sin γ ctg φ) c (cos α - sin α ctg φ) a (cos β + sin β ctg φ) . \end{matrix}

Egyszerűsítés után ebből

\begin{matrix} cos γ + sin γ ctg φ = cos γ - sin γ ctg φ, \end{matrix}

tehát

φ = 90^{\circ} .

Kassai Lóránt (Fazekas M. Főv. Gyak. Gimn. IV. o. t.) dolgozata alapján