Kezdőlap


Feladat:	F.2936	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bajszi István , Csergőffy Tibor , Csermely Zoltán , Csikai Szabolcs , Csörnyei Marianna , Diószeghy Zoltán , Dőtsch András , Égi József , Futó Gábor , Gyarmati Katalin , György András , Horváth Gábor , Hüber Erik , K. L. , Kálmán Tamás , Kóczy László , Kórász Árpád , Kovács Szabolcs , Kucsera Henrik , Markót Mihály , Maróti Attila , Maróti Gábor , Marx Gábor , Mosonyi Milán , Nagy Anett , Németh Ákos , Pete Gábor , Rákóczi Bálint , Réti Géza , Róka Dániel , Rónai András , Szeredi Tibor , Tichler Krisztián , Tóth Zoltán , Zsenei András
Füzet:	1993/május, 209. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Trapézok, Thalesz-kör, Feladat
Hivatkozás(ok):	Feladatok: 1992/december: F.2936

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen az átlók metszéspontja $P$ , az $A D$ , illetve $B C$ felezőpontja pedig 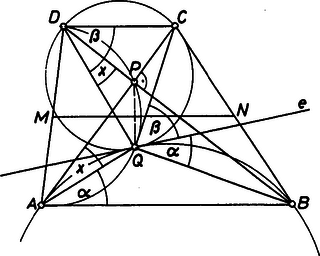$M$ , illetve $N$ .

P

pont illeszkedik

A D

Thalész körére, és ‐ mivel a tükrözés folytán

M P = M Q

‐ a

Q

pont is rajta van

A D

Thalész körén. Ezért

A Q P D

húrnégyszög, így az ábrán

x

-szel jelölt szögek egyenlők. Jelöljük az

A B Q

háromszög köré írt körnek egyik,

Q B

ívéhez tartozó kerületi szöget

α

-val, a

C D Q

köré írt kör

Q C

ívéhez tartozó kerületi szöget pedig

β

-val az ábra szerint. Az

A B P

derékszögű háromszögből

P A B ∢ + P B A ∢ = 90^{\circ}

, és mivel váltószögek,

P B A ∢ = P D C ∢ = β - x .

Így

α + β = α + x + β - x = 90^{\circ}

.
Minthogy

B Q P C

is húrnégyszög,

B Q C ∢ = 90^{\circ}

, tehát

B Q C ∢ = α + β

. Ezért az ábrán

e

-vel jelölt egyenes az

A B Q Δ

köré írt körének és a

C D Q Δ

köré írt körének is érintője.Tehát

e

a két kör közös érintője, ezért a két körülírt kör a

Q

pontban érinti egymást.

Róka Dániel (Bp., Szent István Gimn., IV. o. t.)