Kezdőlap


Feladat:	F.2924	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Adorján Richárd , Csergőffy Tibor , Csörnyei Marianna , Diószeghy Zoltán , Dőtsch András , Futó Gábor , Gyarmati Katalin , György András , Hollósi Szabolcs , Katz Sándor , Kóczy László , Kórász Árpád , Kucsera Henrik , Lengyel Csaba , Maróti Attila , Maróti Gábor , Marx Gábor , Megyesi Zoltán , Németh Ákos , Pete Gábor , Tichler Krisztián , Tóth Zoltán
Füzet:	1993/április, 160 - 162. oldal		PDF \| MathML
Témakör(ök):	Ellipszis egyenlete, Kúpszeletek érintői, Szélsőérték-feladatok differenciálszámítás nélkül, Feladat
Hivatkozás(ok):	Feladatok: 1992/október: F.2924

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen az ellipszis egyenlete $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ , egy ilyen téglalap egyik csúcsa $P (u; v)$ . Először megmutatjuk, hogy a $P$ pontok egy $\sqrt[]{a^{2} + b^{2}}$ sugarú körön helyezkednek el. A $P$ ponton átmenő $m$ iránytangensű egyenes és az ellipszis közös pontjainak koordinátáit az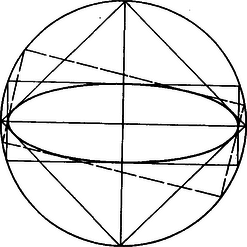

\begin{matrix} \begin{matrix} y = m (x - u) + v \\ \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 \end{matrix} \end{matrix}

egyenletrendszer megoldásai adják:

\begin{matrix} b^{2} x^{2} + a^{2} {(m x - m u + v)}^{2} = a^{2} b^{2}, \end{matrix}

azaz

\begin{matrix} (b^{2} + a^{2} m^{2}) x^{2} + 2 a^{2} m (v - m u) x + (a^{2} m^{2} u^{2} + a^{2} v^{2} - 2 a^{2} m u v - a^{2} b^{2}) = 0. \end{matrix}

1. ábra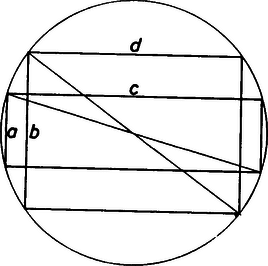

2. ábra

Az egyenes akkor lesz érintő, ha ennek az (

x

-ben másodfokú) egyenletnek a diszkriminánsa zérus, azaz:

\begin{matrix} 0 = {[2 a^{2} m (v - m u)]}^{2} - 4 (b^{2} + a^{2} m^{2}) (a^{2} m^{2} u^{2} + a^{2} v^{2} - 2 a^{2} m u v - a^{2} b^{2}) = \\ = 4 a^{2} \cdot b^{2} [(a^{2} - u^{2}) m^{2} + 2 u v m + b^{2} - v^{2}] . \end{matrix}

Ennek az (

m

-re másodfokú) egyenletnek a gyökei a

P

pontból húzható érintők iránytangesei. Mivel ezek az érintők merőlegesek, a gyökök szorzata

- 1

lesz, tehát

\frac{b^{2} - v^{2}}{a^{2} - u^{2}} = - 1

(ha

a^{2} \neq u^{2}

) vagyis

u^{2} + v^{2} = a^{2} + b^{2}

, amely már

a^{2} = u^{2}

esetén is érvényes. Ez azt jelenti, hogy az érintő téglalap csúcsai rajta vannak az

x^{2} + y^{2} = a^{2} + b^{2}

egyenletű körön.
Most már csak ki kell választanunk az ebbe a körbe írt téglalapok közül az ellipszist érintő legnagyobb és legkisebb kerületűt. Jelöljük két, a körbe írt téglalap oldalait az 2. ábra szerint, ahol ,,

a

'' a legkisebb oldal, továbbá

a < c

és

b \leq d

. Nyilván

{(2 r)}^{2} = a^{2} + c^{2} = b^{2} + d^{2}

, és így

c^{2} - d^{2} = b^{2} - a^{2}

, azaz

c - d = \frac{b + a}{c + d} (b - a)

; tehát a feltételek szerint

c - d < b - a

. Így

2 (a + c) < 2 (b + d)

, tehát annak a téglalapnak a kerülete a kisebb, amelyiknek kisebb a rövidebbik oldala. Mivel az ellipszis köré írt téglalapnak a kistengelynél kisebb oldala nem lehet, azért az a téglalap lesz a legkisebb kerületű, amelynek egyik oldala a kistengely, tehát oldalai párhuzamosak az ellipszis szimmetriatengelyeivel. A legnagyobb pedig akkor lesz a kerület, ha a téglalap négyzet, tehát ha a csúcsai az ellipszis szimmetriatengelyein helyezkednek el.

Tichler Krisztián (Fazekas M. Főv. Gyak. Gimn., IV. o. t.) dolgozata alapján