Kezdőlap


Feladat:	F.2918	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Dienes Péter , Dőtsch András , Markót Mihály , Marx Gábor , Németh Ákos , Pete Gábor
Füzet:	1993/február, 66 - 68. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Forgatva nyújtás, Komplex számok tulajdonságai, Párhuzamos szelők tétele, Feladat
Hivatkozás(ok):	Feladatok: 1992/szeptember: F.2918

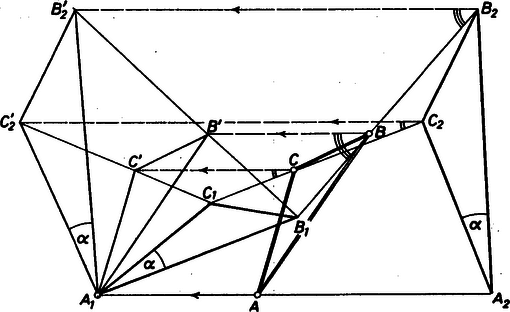
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Toljuk el az $A B C$ és az $A_{2} B_{2} C_{2}$ háromszöget úgy, hogy $A$ és $A_{2}$ képe $A_{1}$ legyen. Használjuk az ábra további jelöléseit. Az eltolás révén

\begin{matrix} A_{1} A = C^{'} C és A_{1} A_{2} = C_{2}^{'} C_{2} . \end{matrix}

(1)

Feltételeinkből következik, hogy

\frac{C_{1} C}{C_{1} C_{2}} = \frac{A_{1} A}{A_{1} A_{2}}

, ezért (1) alapján

\begin{matrix} \frac{C_{1} C}{C_{1} C_{2}} = \frac{C^{'} C}{C_{2}^{'} C} . \end{matrix}

(2)

Az eltolások folytán a két ívvel jelölt szögek megegyeznek. Így a párhuzamos szelők tétele szerint a

C_{1} C C^{'}

és

C_{1} C_{2} C_{2}^{'}

háromszögek hasonlóak. Ezért a

C_{1}

C^{'}

és

C_{2}^{'}

pontok egy egyenesen vannak, és

\begin{matrix} \frac{C_{1} C^{'}}{C^{'} C_{2}^{'}} = \frac{C_{1} C}{C C_{2}} . \end{matrix}

(3)

Ugyanígy megmutatható, hogy

B_{1}

B^{'}

és

B_{2}^{'}

is egy egyenesen van, és

\begin{matrix} \frac{B_{1} B^{'}}{B^{'} B_{2}^{'}} = \frac{B_{1} B}{B B_{2}} = \frac{C_{1} C}{C C_{2}} . \end{matrix}

(4)

Tekintsük most az

A_{1}

középpontú

α

szögű

\frac{A_{1} C_{1}}{A_{1} B_{1}}

arányú forgatva nyújtást. Ez a transzformáció a

B_{1}

pontot a

C_{1}

-be, a

B_{2}^{'}

pontot a

C_{2}^{'}

-be viszi át. Mivel ez egy hasonlósági transzformáció, ezért a

B_{1} B_{2}^{'}

szakasz

B^{'}

osztópontját a

C_{1} C_{2}^{'}

szakasz

C^{'}

osztópontjába viszi át, hiszen (3) és (4) szerint a

B^{'}

pont ugyanolyan arányban osztja az előbbi szakaszt, mint

C^{'}

az utóbbit. Tehát

B^{'} A_{1} C^{'} ∢ = α

, és

\frac{A_{1} C^{'}}{A_{1} B^{'}} = \frac{A_{1} C_{1}}{A_{1} B_{1}}

, ami azt jelenti, hogy

A_{1} B^{'} C^{'}

háromszög hasonló az

A_{1} B_{1} C_{1}

háromszöghöz; de akkor ugyanez áll fenn a vele egybevágó

A B C

háromszögre is.

Megjegyzés. A bizonyítás a komplex számok segítségével is elvégezhető, amint azt ‐ többek között ‐ prof. Walter Janous innsbrucki olvasónk is megjegyezte. Tekintsük e célból a sík egy tetszőlegesen választott pontjából az

A_{i}

B_{i}

C_{i}

pontokba mutató

a_{i}

b_{i}

c_{i}

vektorokat komplex számoknak. A feladat feltételei szerint (valamely

z

komplex számmal)

\begin{matrix} \frac{a_{1} - b_{1}}{a_{1} - c_{1}} = \frac{a_{2} - b_{2}}{a_{2} - c_{2}} = z . \end{matrix}

(5)

Az origóból az

A

B

C

pontokba mutató

a

b

c

vektorok:

\begin{matrix} a = t a_{1} + (1 - t) a_{2}, \\ b = t b_{1} + (1 - t) b_{2}, \\ c = t c_{1} + (1 - t) c_{2}, \end{matrix}

ahol

t

valós szám. Így (5) figyelembevételével

\begin{matrix} \begin{matrix} \frac{a-b}{a-c} & = \frac{t (a_{1} - b_{1}) + (1 - t) (a_{2} - b_{2})}{t (a_{1} - c_{1}) + (1 - t) (a_{2} - c_{2})} = \\ = \frac{t z (a_{1} - c_{1}) + (1 - t) z (a_{2} - c_{2})}{t (a_{1} - c_{1}) + (1 - t) (a_{2} - c_{2})} = z = \frac{a_{i} - b_{i}}{a_{i} - c_{i}}, \end{matrix} \end{matrix}

ami éppen azt jelenti, hogy

A B C

hasonló az

A_{i}

B_{i}

C_{i}

háromszögekhez.