| Feladat: | F.2906 | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Csörnyei Marianna , Szeidl Ádám | ||
| Füzet: | 1993/január, 16. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Lefedések, Ponthalmazok, Terület, felszín, Síkbeli ponthalmazok távolsága, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1992/április: F.2906 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Vegyünk a feladatban szereplő érték helyett -t. Azt fogjuk megmutatni, hogy a síkidomok által lefedett terület biztosan kisebb, mint . (Ebből már következik a feladat állítása.) 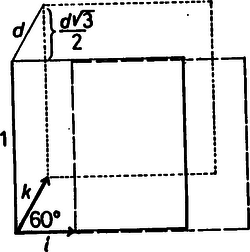 Vizsgáljuk meg most azt, hogy a két eltolással kapott halmaznak van-e közös pontja. Tegyük fel, hogy van, és legyen egy ilyen pont. Ekkor valamely és pontokra és . Ezért a háromszög szabályos, amiért , ez azonban ismét ellentmondás. Azt kapjuk tehát, hogy az és , halmazok közül bármelyik kettő metszete üres. Tekintsük ezután a három halmaz síkbeli elhelyezkedését. Mivel az egységnégyzet részhalmaza, ill. az egységnégyzet i-vel, illetve j-vel való eltoltjának részhalmazai. Ábránkon a három négyzet unióját tüntettük fel, amelynek területe . Ha az és diszjunkt és egyenlő területű, a halmazok területe külön-külön , akkor , tehát . Ezzel az állítást igazoltuk. Szeidl Ádám (Miskolc, Földes Ferenc Gimn., II. o. t.) |