Kezdőlap


Feladat:	F.2905	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Csermely Zoltán , Csörnyei Marianna , Faragó Gergely , Futó Gábor , Kálmán Tamás , Marx Gábor , Megyesi Zoltán , Párniczky Benedek , Pete Gábor , Valkó Benedek
Füzet:	1993/március, 113 - 114. oldal		PDF \| MathML
Témakör(ök):	Transzformációk fixpontjai, fixalakzatai, Transzformációk szorzata, Síkgeometriai szerkesztések, Feladat
Hivatkozás(ok):	Feladatok: 1992/április: F.2905

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tekintsük a feladatot megoldottnak. Jelöljük a háromszög csúcsait $A, B, C,$ -vel, a szabályos $n$ -szögek középpontjait pedig $X, Y, Z$ -vel az ábra szerint.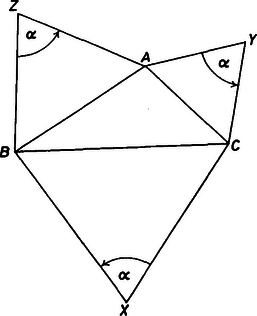

Y

körüli

α = \frac{2 π}{n}

(irányított) szögű forgatás

A

-t

C

-be, az

X

körüli

\frac{2 π}{n}

szögű forgatás

C

-t

B

-be, végül a

Z

körüli

\frac{2 π}{n}

szögű forgatás

B

-t

A

-ba viszi át. Tehát a három forgatás egymásutánjának (szorzatának) az

A

fixpontja. Ismeretes, hogy egy

α, β

és

γ

szögű forgatás szorzata egy

α + β + γ

szögű forgatás, ha

α + β + γ \neq 2 k π

, illetve eltolás vagy identitás, ha

α + β + γ = 2 k π .

Ennek bizonyítása ‐ az eredőforgatás középpontjának szerkesztési módjával együtt ‐ megtalálható Rácz János: Matematika feladatok ‐ ötletek ‐ megoldások c. könyvének 313‐315. oldalán. A feladatot ezután úgy oldjuk meg, hogy megkeressük az

Y

X

illetve

Z

pontok körüli

\frac{2 π}{n}

szögű forgatások szorzatának fixpontját, ami esetünkben az

A

pont lesz. Mivel az

n = 3

esetben a három forgatás szögének összege

3 \cdot \frac{2 π}{3} = 2 π

, tegyük fel egyelőre, hogy

n ⩾ 4

. Forgassuk el a sík egy tetszőleges

P

pontját

Y,

majd

X,

majd pedig

Z

körül

\frac{2 π}{n}

-nel. Legyen

P

képe

P'

. Ha

P \equiv P'

, akkor

P

éppen az

A

pont, ha

P ≢ P'

, akkor az

A

pontot a

P P'

felező merőlegesén kell keresnünk úgy, hogy

P A P' ∢ = 3 \cdot \frac{2 π}{n}

legyen. (Az

A

pont megszerkesztésének módját az előbb említett könyv hivatkozott lapjain is megtalálhatjuk.) Ezután a

C

pontot az

A

pont

Y

körüli

\frac{2 π}{n}

. szöggel,

B

-t az

A

pont

Z

körüli

- \frac{2 π}{n}

szöggel való elforgatottjaként kapjuk. Mivel az

n ⩾ 4

esetben

A

a forgatás (egyetlen) fixpontja, a feladatnak egy megoldása van.
Az

n = 3

esetben az

A B C

háromszög oldalaira kifelé írt szabályos háromszögek középpontjai szabályos háromszöget alkotnak. (Ennek bizonyítása megtalálható a Geometriai feladatok gyűjteménye I. 3160. feladat megoldásában.) Ez azt jelenti, hogy ha

n = 3

, a feladat csak akkor oldható meg, ha az

X Y Z

háromszög szabályos. Megmutatjuk, hogy ilyenkor viszont végtelen sok megoldás van. Legyen

A_{1} B_{1} C_{1}

tetszőleges háromszög, az oldalaira kifelé szerkesztett szabályos háromszögek középpontjai

X_{1}, Y_{1}, Z_{1}

. Az előbbiek szerint az

X_{1} Y_{1} Z_{1}

háromszög szabályos. Tekintsük azt a hasonlóságot, amelyik az

X_{1} Y_{1} Z_{1}

háromszöget az

X Y Z

-be viszi át. Legyen ebben a hasonlóságban az

A_{1} B_{1} C_{1}

háromszög képe az

A B C

háromszög. Az

A B C

háromszög feladatunk egy megoldása.

Megjegyzés: Feladatunkkal egy időben Gy. 2772. gyakorlatként kitűztük az

n = 4

-nek megfelelő esetet. A gyakorlat megoldása az 1992. évi 8‐9. számban megjelent. Az ott közölt második megoldás szinte szóról-szóra alkalmazható akkor is, ha

n > 4.