Kezdőlap


Feladat:	F.2893	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Csörnyei Marianna , Faragó Gergely , Futó Gábor , Kálmán Tamás , Nyúl László , Párniczky Benedek , Stőhr Lóránt , Újváry-Menyhárt Zoltán
Füzet:	1992/szeptember, 256 - 257. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Geometriai egyenlőtlenségek, Magasságvonal, Súlypont, Számtani-mértani egyenlőtlenségek, Feladat
Hivatkozás(ok):	Feladatok: 1992/február: F.2893

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen a feladatban szereplő belső pont $P$ . Húzzunk $P$ -n át párhuzamosokat a háromszög oldalaival.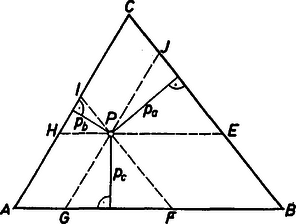

Használjuk az ábra további jelöléseit is. A

H P I

G F P

P E J

háromszögek hasonlóak az

A B C

háromszöghöz, a hasonlóság aránya legyen rendre

α

β

γ

. Az ábráról leolvasható, hogy

A B = A G + G F + F B = H P + G F + P E = α \cdot A B + β \cdot A B + γ \cdot A B

, amiből azonnal következik, hogy

α + β + γ = 1

. A számtani és mértani közép közti összefüggés szerint

α \cdot β \cdot γ \leq {(\frac{α + β + γ}{3})}^{3} = \frac{1}{27}

, amit

m_{a} m_{b} m_{c}

-vel szorozva:

α \cdot m_{a} \cdot β \cdot m_{b} \cdot γ \cdot m_{c} \leq \frac{m_{a} m_{b} m_{c}}{27}

.
Ebből

27 p_{a} \cdot p_{b} \cdot p_{c} \leq m_{a} m_{b} m_{c}

; fölhasználtuk, hogy pl.

α m_{a} = p_{a}

. Ezzel a feladat állítását bebizonyítottuk. Egyenlőség akkor áll fenn, ha

α

β

γ

számtani és mértani közepe megegyezik, tehát ha

α = β = γ = \frac{1}{3}

, azaz

p_{a} = \frac{m_{a}}{3}

p_{b} = \frac{m_{b}}{3}

p_{c} = \frac{m_{c}}{3}

. Ez pontosan akkor következik be, ha

P

a háromszög súlypontja.

Ujváry-Menyhárt Zoltán (Fazekas M. Főv. Gyak. Gimn., IV. o. t.)

II. megoldás. Jelöljük az

A B C

háromszög területét

t

-vel, a

B C P

A B P

C A P

háromszögek területét pedig

t_{1}

t_{2}

t_{3}

-mal. Világos, hogy

t_{1} + t_{2} + t_{3} = t

. A számtani és mértani közép közti egyenlőtlenség szerint

\begin{matrix} (\frac{t}{3})^{3} = (\frac{t_{1} + t_{2} + t_{3}}{3})^{3} \geq t_{1} t_{2} t_{3} . \end{matrix}

\frac{a \cdot m_{a}}{2} = \frac{b \cdot m_{b}}{2} = \frac{c \cdot m_{c}}{2} = t

összefüggések alapján

t^{3} = \frac{a b c \cdot m_{a} \cdot m_{b} \cdot m_{c}}{8}

. Hasonlóan kapjuk, hogy

t_{1} t_{2} t_{3} = \frac{a b c \cdot p_{a} \cdot p_{b} \cdot p_{c}}{8}

, hiszen pl.

t_{1} = \frac{a p_{a}}{2}

. A két utóbbi összefüggés szerint (1) így alakul:

\begin{matrix} \frac{a b c \cdot m_{a} \cdot m_{b} \cdot m_{c}}{8 \cdot 27} \geq \frac{a b c \cdot p_{a} \cdot p_{b} \cdot p_{c}}{8} & , amiből \\ m_{a} m_{b} m_{c} \geq 27 \cdot p_{a} \cdot p_{b} \cdot p_{c} & . \end{matrix}

Egyenlőség pontosan akkor lesz, ha (1)-ben egyenlőség áll fenn, tehát ha

t_{1} = t_{2} = t_{3} = \frac{t}{3}

, azaz, ha

P

a háromszög súlypontja.