Kezdőlap


Feladat:	F.2875	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Csörnyei Marianna , Kálmán Tamás , Kerekes Balázs , Levente Gábor , Szendrei Tamás
Füzet:	1992/november, 364 - 365. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Pont körüli forgatás, Geometriai transzformációk, Síkgeometriai számítások trigonometria nélkül háromszögekben, Síkgeometriai szerkesztések, Feladat
Hivatkozás(ok):	Feladatok: 1991/november: F.2875

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelölje $O$ az $A_{1} A_{2} A_{3}$ szabályos háromszög középpontját. Tegyük fel, hogy $C_{1}, C_{2}, C_{3}$ megoldása a feladatnak.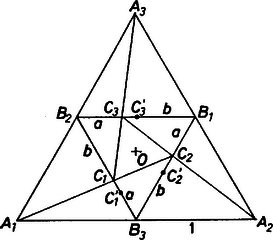

1. ábra

Megmutatjuk, hogy ekkor más megoldás nem létezik. Ha ugyanis a

C'_{1}, C'_{2}, C'_{3}

pontok is eleget tesznek a feladat követelményeinek, akkor például

C'_{3} \neq C_{3}

. Tételezzük fel, hogy

C'_{3}

C_{3} B_{1}

szakasz belső pontja. Mivel

A_{3}, C'_{3}, C'_{1}

is egy egyenesbe esnek, azért

C'_{1}

C_{1} B_{3}

belsejében fekszik. Hasonlóan

A_{1}, C'_{1}, C'_{2}

is egy egyenesen helyezkednek el, ezért

C'_{2}

csak

B_{3} C_{2}

belsejében lehet. Így azonban az

A_{2} C_{3}

egyenes elválasztja a

C'_{2}, C'_{3}

pontokat, tehát

A_{2}, C'_{2}, C'_{3}

nem lehetnek egy egyenesen. Ugyanerre az eredményre jutunk abban az esetben is, ha

C'_{3}

B_{2} C_{3}

szakasz belsejében található; ezzel beláttuk, hogy a feladat megoldása (ha egyáltalán létezik) egyértelmű.
Forgassuk el az

A_{1}, A_{2}, A_{3}

, valamint a

C_{1}, C_{2}, C_{3}

pontokat

O

körül

120^{\circ}

-kal. Mivel az

A_{1}, A_{2}, A_{3}

pontok egymás elforgatottjai, azért a

C_{1}, C_{2}, C_{3}

képei ismét egy megoldást szolgáltatnak. Az egyértelműség miatt ez csak úgy lehetséges, hogy

C_{1}, C_{2}, C_{3}

egymásba mennek át az elforgatás során, vagyis a

C_{1} C_{2} C_{3}

háromszög is szabályos. Ebből következik, hogy

\begin{matrix} C_{2} B_{1} = C_{3} B_{2} = C_{1} B_{3} és & (1) \\ B_{3} C_{2} = B_{1} C_{3} = B_{2} C_{1} . & (2) \end{matrix}

Jelöljük az (1)-ben és (2)-ben szereplő szakaszok hosszát

a

-val, illetve

b

-vel, a

B_{1} B_{2} B_{3}

háromszög oldala pedig legyen egységnyi. A

C_{3} C_{2} B_{1}

és

A_{2} C_{2} B_{3}

háromszögek hasonlók, mert szögeik páronként megegyeznek. Ezért

a : b = b : 1

, és mivel

a + b = 1

\begin{matrix} a : b = b : (a + b) . \end{matrix}

(3)

Ez azt jelenti, hogy pl. a

C_{2}

pont a

B_{1} B_{3}

szakaszt az aranymetszés szerint osztja. A (3) egyenletet így írhatjuk:

b^{2} = a (a + b)

és mivel

a = 1 - b, b^{2} = 1 - b

. Ebből az egyenletből

b = \frac{- 1 \pm \sqrt[]{5}}{2}

, mivel

b

pozitív szám,

b = \frac{- 1 + \sqrt[]{5}}{2}

. (A

b

szakasz szerkesztését a 2. ábrán láthatjuk.)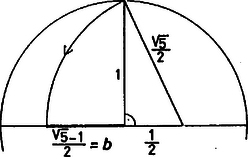

2. ábra

Ha pl. a

C_{2}

pontot a

B_{1} B_{3}

szakaszon (3)-nak megfelelően megszerkesztjük, a

B_{1}

és

B_{3}

-nál lévő

60^{\circ}

-os szögek és az ezeket közbezáró oldalak arányának megegyezése réven az

A_{2} C_{2} B_{3}

és

C_{3} C_{2} B_{1}

háromszögek hasonlóak lesznek. Ennek következménye, hogy az

A_{2}, C_{2}, C_{3}

pontok egy egyenesre illeszkednek. Hasonlóan igaz az

A_{3}

C_{3}

C_{1}

és

A_{1}

C_{1}

C_{2}

ponthármasokra, tehát szerkesztésünk helyes.

Megjegyzés. Vizsgáljuk meg azt az esetet, amikor az

A_{1} A_{2} A_{3}

háromszög nem szabályos. Ismeretes ‐ azok számára, akik tanultak az affin transzformációkról ‐ hogy bármely két háromszöghöz egyértelműen létezik egy olyan affinitás (egyenestartó transzformáció), amely az egyik háromszög csúcsait a másik csúcsaiba viszi át. Tudjuk továbbá, hogy az affin transzformáció egy egyenes három pontjának osztási arányát (az osztóviszonyt) megtartja, ezért pl. felezőpontot felezőpontba, szakasz aranymetszés szerinti osztópontját aranymetszés szerinti osztópontba visz át. Így egy szabályos háromszöghöz és egy tetszőleges

A_{1} A_{2} A_{3}

háromszöghöz található a fenti tulajdonságokkal rendelkező affin transzformáció. Ez azt jelenti, hogy a szabályos háromszögre talált eljárás a

C_{1}

C_{2}

C_{3}

pontok megszerkesztésére bármely háromszögnél alkalmazható.

Csörnyei Marianna (Főv. Fazekas M. Gyak. Gimn., II. o. t.)